Konträra satser
| Härledningsbegrepp |
|---|
| Närliggande begrepp |
Konträra satser eller konträra påståenden, är begrepp hämtade från predikatlogiken. Två påståenden är konträra, om de av logiska grunder inte båda kan vara sanna, men båda kan vara falska. Om det ena påståendet är sant, följer således att det andra är falskt.
Eftersom predikatlogiken liksom satslogiken är ett formellt system, gäller att slutsatser som kan härledas i ett sådant inte har något att göra med de språkliga uttryckens mening eller betydelse, utan endast bestäms av relationerna mellan de symboler av vilka satserna är uppbyggda.
Påståendena, A: Alla svanar är vackra och E: Inga svanar är vackra, är konträra. Att så är fallet följer enkom av logik och syntax. Om man håller den ena satsen för sann tvingas man, av uteslutande logiska överväganden, att hålla den andra för falsk. Skulle någon vilja hävda att båda satserna är falska, så lägger åtminstone inte de formella logiska reglerna något hinder i vägen för detta ställningstagande. : Någon svan är inte vacker och : Någon svan är vacker, kan således båda vara sanna.
En vanlig källa till förvirring i detta sammanhang är att, outtalat eller omedvetet, tillämpa formella logiska system och begrepp på någon oförgriplig verklighet, där påståendens sanningshalt hålls för självklara.
Följande två påståenden är inte konträra, men väl kontradiktoriska: I: Några svanar är vita, E: Inga svanar är vita. Båda påståendena kan inte vara sanna och ej heller kan båda vara falska.
Om två påståenden är konträra så kan de inte vara kontradiktoriska och ej heller kan två påståenden, som är kontradiktoriska vara konträra.
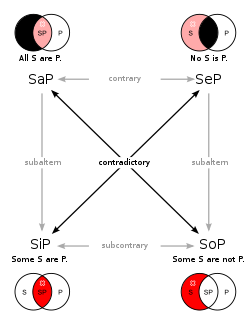
Satsbenämningarna A, E, I och O hänför sig till den så kallade Aristoteliska kvadraten. Av figuren framgår att endast påståenden, där det ena är på formen A och det andra på formen E är konträra.
Se även
[redigera | redigera wikitext]Källor
[redigera | redigera wikitext]- Geoffrey Hunter, Metalogic, An Introduction to the Metatheory of Standard First-Order Logic, MacMillan, London 1971.
- H. Kahane, Logic and Philosophy, Wadsworth 1969.
- Georg Henrik von Wright, Logik, filosofi och språk, Berlingska, Lund 1957.


