Dedekinds η-funktion i komplexa planet. Inom matematiken är Dedekinds etafunktion , uppkallad efter Richard Dedekind , en viss modulär form av vikt 1/2. För komplexa tal τ med positiv imaginär del låtq = exp(2πiτ). Då definieras Dedekinds etafunktion som
η
(
τ
)
=
e
π
i
τ
12
∏
n
=
1
∞
(
1
−
q
n
)
.
{\displaystyle \eta (\tau )=e^{\frac {\pi {\rm {{i}\tau }}}{12}}\prod _{n=1}^{\infty }(1-q^{n}).}
Etafunktionen är analytisk i övre planhalvan men kan inte fortsättas analytiskt utanför den.
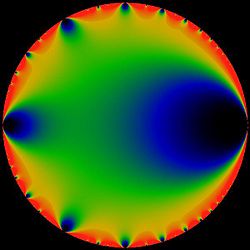
Absoluta värdet av Eulers funktion i enhetsskivan sådan att svart = 0, röd = 4 Diskriminantens reella del som en funktion av q . Etafunktionen satisfierar funktionalekvationerna
η
(
τ
+
1
)
=
e
π
i
12
η
(
τ
)
,
{\displaystyle \eta (\tau +1)=e^{\frac {\pi {\rm {i}}}{12}}\eta (\tau ),\,}
η
(
−
1
τ
)
=
−
i
τ
η
(
τ
)
.
{\displaystyle \eta (-{\tfrac {1}{\tau }})={\sqrt {-{\rm {i}}\tau }}\eta (\tau ).\,}
Mer generellt, antag att a , b , c , d är heltal med ad − bc = 1, sådana att
τ
↦
a
τ
+
b
c
τ
+
d
{\displaystyle \tau \mapsto {\frac {a\tau +b}{c\tau +d}}}
är en transformation i modulära gruppen . Vi kan anta att antingen c > 0 eller c = 0 och d = 1. Då är
η
(
a
τ
+
b
c
τ
+
d
)
=
ϵ
(
a
,
b
,
c
,
d
)
(
c
τ
+
d
)
1
2
η
(
τ
)
,
{\displaystyle \eta \left({\frac {a\tau +b}{c\tau +d}}\right)=\epsilon (a,b,c,d)(c\tau +d)^{\frac {1}{2}}\eta (\tau ),}
där
ϵ
(
a
,
b
,
c
,
d
)
=
e
b
i
π
12
(
c
=
0
,
d
=
1
)
;
{\displaystyle \epsilon (a,b,c,d)=e^{\frac {b{\rm {i}}\pi }{12}}\quad (c=0,d=1);}
ϵ
(
a
,
b
,
c
,
d
)
=
e
i
π
[
a
+
d
12
c
−
s
(
d
,
c
)
−
1
4
]
(
c
>
0
)
.
{\displaystyle \epsilon (a,b,c,d)=e^{{\rm {i}}\pi [{\frac {a+d}{12c}}-s(d,c)-{\frac {1}{4}}]}\quad (c>0).}
Här betecknar
s
(
h
,
k
)
{\displaystyle s(h,k)\,}
Dedekindsumman
s
(
h
,
k
)
=
∑
n
=
1
k
−
1
n
k
(
h
n
k
−
⌊
h
n
k
⌋
−
1
2
)
.
{\displaystyle s(h,k)=\sum _{n=1}^{k-1}{\frac {n}{k}}\left({\frac {hn}{k}}-\left\lfloor {\frac {hn}{k}}\right\rfloor -{\frac {1}{2}}\right).}
η
(
i
)
=
Γ
(
1
4
)
2
π
3
/
4
{\displaystyle \eta (i)={\frac {\Gamma \left({\frac {1}{4}}\right)}{2\pi ^{3/4}}}}
η
(
1
2
i
)
=
Γ
(
1
4
)
2
7
/
8
π
3
/
4
{\displaystyle \eta \left({\tfrac {1}{2}}i\right)={\frac {\Gamma \left({\frac {1}{4}}\right)}{2^{7/8}\pi ^{3/4}}}}
η
(
2
i
)
=
Γ
(
1
4
)
2
11
/
8
π
3
/
4
{\displaystyle \eta (2i)={\frac {\Gamma \left({\frac {1}{4}}\right)}{2^{{11}/8}\pi ^{3/4}}}}
η
(
4
i
)
=
−
1
+
2
4
Γ
(
1
4
)
2
29
/
16
π
3
/
4
{\displaystyle \eta (4i)={\frac {{\sqrt[{4}]{-1+{\sqrt {2}}}}\;\Gamma \left({\frac {1}{4}}\right)}{2^{{29}/16}\pi ^{3/4}}}}
Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia , Dedekind eta function , 7 mars 2014 . Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (2 ed), Graduate Texts in Mathematics 41 (1990), Springer-Verlag, ISBN 3-540-97127-0 Se kapitel 3.
Neil Koblitz, Introduction to Elliptic Curves and Modular Forms (2 ed), Graduate Texts in Mathematics 97 (1993), Springer-Verlag, ISBN 3-540-97966-2 








![{\displaystyle \epsilon (a,b,c,d)=e^{{\rm {i}}\pi [{\frac {a+d}{12c}}-s(d,c)-{\frac {1}{4}}]}\quad (c>0).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/067a2c0c181e24d90a624dbeb42ffaf82cc550f9)





![{\displaystyle \eta (4i)={\frac {{\sqrt[{4}]{-1+{\sqrt {2}}}}\;\Gamma \left({\frac {1}{4}}\right)}{2^{{29}/16}\pi ^{3/4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1fc81d5abeb5174c9c10d1e25abf27e22774055)