Vinkel
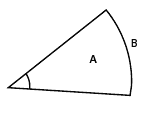
En vinkel eller ett vinkelområde är ett område av ett plan, begränsat av två strålar, det vill säga delar av räta linjer som skär varandra i en punkt.[1] Strålarna utgör vinkelområdets rand, och kallas för vinkelns ben. Skärningspunkten (och ändpunkten för strålarna) kallas för vinkelspets. Normalt markeras en vinkel med en vinkelbåge. Vinkelbegreppet används inom trigonometri och geometri.
För att mäta vinklar ritas en cirkelbåge med centrum i vinkelspetsen. Radianmåttet för vinkeln är längden av bågen mellan vinkelbenen dividerad med cirkelns radie. Vanligen uttrycks dock vinkeln i grader
Symbolen för enheten grad är en lite upphöjd cirkel (°).
Ibland, men inte så ofta, förekommer gradmåttet gon (nygrader).
I militära sammanhang har man använt vinkelmåttet streck (betecknas med en apostrof:'), utgående från att en meters sidoförskjutning på 1000 meters håll är ett streck. Av praktiska skäl avrundas 2π·1000 till 6300, och det går då 6300' på ett varv. Den avrundningen gjordes tidigare i Sverige, i andra länder förekommer det andra praktiska avrundningar till bland annat 6000 eller 6400 streck på ett varv. Det senare används numera i Sverige under beteckningen mils.
| Namn | Varv | Grader | Radianer | Gon (nygrader) | Bågminuter | Bågsekunder |
|---|---|---|---|---|---|---|
| Spetsig | (0,1⁄4) | (0,90)° | (0,1⁄2π) | (0,100)g | (0;1,5)′ | (0,1575)' |
| Rät | 1⁄4 | 90° | 1⁄2π | 100g | 1,5′ | 1575' |
| Trubbig | (1⁄4,1⁄2) | (90,180)° | (1⁄2π,π) | (100,200)g | (1,5;3)′ | (1575,3150)' |
| Rak | 1⁄2 | 180° | π | 200g | 3′ | 3150' |
| Reflex | (1⁄2,1) | (180,360)° | (π,2π) | (200,400)g | (3,6)′ | (3150,6300)' |
| Perigon | 1 | 360° | 2π | 400g | 6′ | 6300' |
En normal är en linje som skär en given linje eller kurva i rät vinkel. "Rätvinklig mot" betecknas ⊥ (se figur 1).
Cirkeln
[redigera | redigera wikitext]En grad (förtydligat vinkelgrad), vanligtvis betecknad med °, är ett mått på plana vinklar eller en position på en storcirkel (en cirkel på en sfär med mittpunkt som sammanfaller med sfärens mittpunkt) i en sfär, ex. jorden el. planetrörelser runt andra himlakroppar. En grad motsvarar 1/360 dels varv runt cirkelns – eller sfärens – omkrets (jfr jordens koordinatsystem).
- 1° motsvarar 1/360 varv runt periferin
- minuter, betecknas med ett primtecken (′), 1 minuter = (1/60)° = 1/21 600 varv,
- sekunder, betecknas med dubbla primtecken (″), 1 sekund = 1/60 minut = 1/1 296 000 varv.
Ex. motsvarar 40°12′13″ 40 grader, 12 minuter och 13 sekunder, eller ungefär 11/100 varv runt jorden.
I matematiska och tekniska sammanhang används ofta radianer. En grad motsvarar π/180 rad, och ett varv runt cirkel motsvarar 2π radianer.
Ett modernt vinkelmått anpassat efter decimala systemet är nygrader. 1 nygrad motsvarar 1/400 varv runt periferin:
- 90° motsvarar 100 nygrader (100g),
- 1g indelas i 100 nyminuter (100c),
- 1c indelas i 100 nysekunder (100cc).
Annat som mäts i vinkelenheter
[redigera | redigera wikitext]Vinklar är alltid mellan 0 och 360, men gradtal större än 360° och negativa värden är tänkbara i andra sammanhang:
- Vinkel - se ovan
- Riktning:
- Kompassriktning (bäring) anges som grader för den vinkel som bildas räknat medurs från nordriktningen. Öster=90°, söder=180°, väster=270° och norr=360° eller 0°.
- Numrering av flygets start- och landningsbanor består av kompassriktningen avrundad till närmaste tiotals grader. En bana i öst-västlig riktning har då numret 09 vid start mot öster och 27 vid start mot väster.
- I ett polärt koordinatsystem räknas riktningen moturs från positiva första axeln (oftast x-axeln). I dessa fall kan man tänka sig riktningar i olika intervall såsom 0°<v<360°, -90°<v<270° eller -180°<v<180°.
- Vridning. Här kan vilka som helst värden tänkas. En vridning på 450° resulterar i samma riktning som en vridning på 90°, men först efter ett helt varvs vridning. (Alltså den vridning som minutvisaren på en klocka gör på 75 minuter.)
- Växelström. Fasförskjutning mellan sinusformade elektriska signaler. Två tidsförskjutna spänningar tecknas och . Vinkelfrekvensen är , där är frekvensen i Hertz. Fasskillnaden uttrycks i grader eller radianer. Förskjutningen mellan signalerna kan även uttryckas som en tid .
Konvertering mellan vinkelenheter
[redigera | redigera wikitext]För att konvertera en vinkel från en enhet till en annan använder man enklast tumregeln tillenhet genom frånenhet. Till exempel blir det för omvandling från gon till grader:
Vinkelmåttens historia
[redigera | redigera wikitext]Gradmåttet där varvet delas in i 360 grader härstammar från det babyloniska räknesystemet, där talbasen var 60. Inte oväsentligt i sammanhanget är att ett år är drygt 360 dagar långt.
När matematisk analys utvecklades på 1600-talet, sökte man efter ett för differentialkalkylen lämpligare universellt mått, och införde radianbegreppet.
I decimalsystemets anda införde man på 1800-talet i Frankrike nygrader, eftersom 100 nygrader på ett kvartsvarv ser mer "naturligt" ut än 90 grader. Det underlättar vissa huvudräkningar (varje kvadrant har sin hundratalssiffra). Man slipper räknandet med sextiondedelar när man arbetar med bråkdelar av en grad. Nygrader har främst använts inom geodesin, men inom andra områden har enheten inte fått det genomslag som man en gång förväntade sig.
Det universella vinkelmåttet är radianer eftersom detta tar bort godtyckligheten i talet 360 inom gradsystemet och eftersom trigonometriska funktioner kan deriveras enkelt samt därmed uttryckas med enkla taylorserier om deras argument är specificerat i radianer. Internationella måttenhetssystemet (SI) använder radianer som (den härledda) enheten för vinklar.
Typer av vinklar
[redigera | redigera wikitext]- En vinkel som är mindre än en rät vinkel (90°) kallas spetsig vinklel.
- En vinkel som är större än en rät vinkel (90°), men mindre än rak vinkel (180°), kallas trubbig vinklel.
- Om summan av två vinklar är en rät vinkel (90°) brukar vinklarna kallas komplementvinklar.
- Om summan av två vinklar är en rak vinkel (180°) brukar vinklarna kallas supplementvinklar.
- Om summan av två vinklar är 360° brukar vinklarna kallas explementvinklar.
Den linje, som skär två eller flera andra linjer, kallas transversal (tvärlinje) till linjerna. I varje skärningspunkt bildas fyra vinklar.
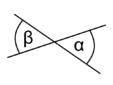
- Två räta linjer som korsar varandra bildar fyra vinklar. Varje vinkel är likadan som motstående vertikalvinkel (se figur 2a), medan de övriga paren kallas sidovinklar och är supplementvinklar (se ovan).
- Om en rät linje korsar två parallella linjer bildas fler relationer. Likbelägna vinklar är lika stora, liksom alternatvinklar. Alternatvinklar är de vinklar som i figuren är vertikalvinklar till de markerade (se figur 2b), dvs. de ligger mellan de parallella linjerna men på var sin sida om den skärande linjen.
- Summan av en triangels (inre tre) vinklar bildar beloppet 180°.
- Summan av en fyrhörnings (inre fyra) vinklar bildar beloppet 360°
- Summan av en n-sidig polygons (inre n) vinklar bildar beloppet (n - 2)·180° eller (n - 2)·π rad.
- Figur 2a. Två räta linjer som korsar varandra i en gemensam punkt.
Källor
[redigera | redigera wikitext]- ^ Sidorov, L.A. (2001), ”Angle”, i Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104
Externa länkar
[redigera | redigera wikitext] Wiktionary har ett uppslag om vinkel.
Wiktionary har ett uppslag om vinkel. Wikisource har originalverk som rör Vinkel.
Wikisource har originalverk som rör Vinkel.  Wikimedia Commons har media som rör vinkel.
Wikimedia Commons har media som rör vinkel. Wikidata har data som rör Vinkel.
Wikidata har data som rör Vinkel.
| |||||||||||||
|