Prüfergrupp

Prüfer-2-gruppen.

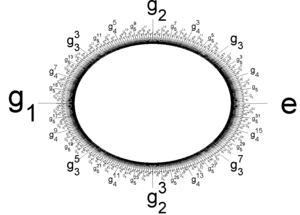
Inom matematiken är Prüfer-p-gruppen (även känd som p-kvasicykliska gruppen, p^∞-gruppen eller Z(p^∞) för ett primtal p den unika p-gruppen där varje element har p skilda p-te rötter. Gruppen är uppkallad efter Heinz Prüfer. Den är en uppräknelig abelsk grupp och är till hjälp då man klassificerar oändliga abelska grupper.

Konstruktioner av Z(p^∞)

Prüfer-p-gruppen kan identifieras med delgruppen av cirkelgruppen U(1) bestående av alla pⁿ-te enhetsrötter med n ett icke-negativt heltal:

$\mathbf {Z} (p^{\infty })=\{\exp(2\pi im/p^{n})\mid m\in \mathbf {Z} ^{+},\,n\in \mathbf {Z} ^{+}\}.\;$

Gruppoperationen är multiplikation med komplexa tal.

Alternativt kan Prüfer-p-gruppen ses som Sylow p-delgruppen av kvotgruppen Q/Z, bestående av de element vars ordning är en potens av p:

$\mathbf {Z} (p^{\infty })=\mathbf {Z} [1/p]/\mathbf {Z}$

(där Z[1/p] betecknar gruppen av alla rationella tal vars nämnare är en potens av p, med addition av rationella tal som gruppoperation).

Prüfer-p-gruppen kan även beskrivas som

$\mathbf {Z} (p^{\infty })=\mathbf {Q} _{p}/\mathbf {Z} _{p}$

där Q_p betecknar additiva gruppen av p-adiska tal och Z_p är delgruppen av p-adiska heltal.

Prüfer-p-gruppen har presentationen

$\mathbf {Z} (p^{\infty })=\langle \,g_{1},g_{2},g_{3},\ldots \mid g_{1}^{p}=1,g_{2}^{p}=g_{1},g_{3}^{p}=g_{2},\dots \,\rangle .$

Här är gruppoperationen i Z(p^∞) skriven som multiplikation.

Källor

Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Prüfer group, 18 januari 2015.

• Jacobson, Nathan (2009). Basic algebra. "2" (2nd). Dover. ISBN 978-0-486-47187-7. 
• Pierre Antoine Grillet (2007). Abstract algebra. Springer. ISBN 978-0-387-71567-4. 
• Kaplansky, Irving (1965). Infinite Abelian Groups. University of Michigan Press. 
• N.N. Vil'yams (2001), ”Quasi-cyclic group”, i Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104 .