Hoppa till innehållet

Mathematics: From the Birth of Numbers

Lägg till länkar
Från Wikipedia

Mathematics: From the Birth of Numbers är en omfattande översiktsbok om matematiken författad av den svenske kirurgen och anestesiologen Jan Gullberg[1] utgiven av W. W. Norton år 1997 (ISBN 039304002X). Boken tog tio år att skriva för Gullberg och upptog en stor del av hans fritid.[2][3] Boken blev en stor framgång och dess första upplaga på 17 000 exemplar såldes slut inom sex månader.[2]

Innehåll

[redigera | redigera wikitext]

Bokens 1093 sidor behandlar följande ämnen:

  1. Tal och språk (Numbers and Language)
  2. Talsystem (Systems of Numeration)
  3. Typer av tal (Types of Numbers)
  4. Matematikens hörnstenar (Cornerstones of Mathematics)
  5. Kombinatorik (Combinatorics)
  6. Symbollogik (Symbolic Logic)
  7. Mängdteori (Set Theory)
  8. Introduktion till sekvenser och serier (Introduction to Sequences and Series)
  9. Ekvationsteori (Theory of Equations)
  10. Introduktion till funktioner (Introduction to Functions)
  11. Overtyr till geomertrierna (Overture to the Geometries)
  12. Elementär geometri (Elementary Geometry)
  13. Trigonometri (Trigonometry)
  14. Hyperboliska funktioner (Hyperbolic Functions)
  15. Analytisk geometri (Analytic Geometry)
  16. Vektoranalys (Vector Analysis)
  17. Fraktaler (Fractals)
  18. Matriser och determinanter (Matrices and Determinants)
  19. Entré till kalkyllära (Embarking on Calculus)
  20. Introduktion till differentialkalkyl (Introduction to Differential Calculus)
  21. Introduktion till integralkalkyl (Introduction to Integral Calculus)
  22. Potensserier (Power Series)
  23. Obestämda gränsvärden (Indeterminate Limits)
  24. Återbesök hos de komplexa talen (Complex Numbers Revisited)
  25. Extrema och kritiska punkter (Extrema and Critical Points)
  26. Båglängd (Arc Length)
  27. Centeroider (Centroids)
  28. Area (Area)
  29. Volym (Volume)
  30. Rörelse (Motion)
  31. Harmonisk analys (Harmonic Analysis)
  32. Approximationsmetoder (Methods of Approximation)
  33. Sannolikhetsteori (Probability Theory)
  34. Differentialekvationer (Differential Equations)

Mottagande

[redigera | redigera wikitext]

Arnold Allen, som recenserade Mathematics: From the Birth of Numbers i The American Mathematical Monthly, skrev att även om det finns många värdefulla böcker som skulle kunna göra anspråk på titeln som främsta översikt av matematiken, "är Gullberg's bok helt klart den sammantagna vinnaren. ... Den är enastående att läsa. Jag tar den med mig vart jag än reser."[4] Allen uttrycker att boken har "speciell charm" och utnyttjar marginalen på innovativt sätt och ger “excellenta citat och kvickheter" genom hela verket.[4] Hans favouritkapitel är "Matematikens hörnstenar", som han tycker skulle tilltala både nybörjare och “äldre händer”.[4] Han erkänner sin förvåning över Gullbergs beskrivning av en alternativ metod med penna och papper för multiplikation jämfört med den som vi alla lär oss i skolan, nämligen den egyptiska metoden kallad duplation, och han är förtjust över den "ryska bond-multiplikationsmetoden” omfattande "successiva duplationer och jämkningar".[4] Han beundrar den "effektiva" babyloniska metoden för att beräkna kvadratrötter genom utnyttjande av division och medelvärden. Från Gullberg fick han också lära sig hur man multiplicerar och dividerar med hjälp av en abakus.[4]

Königsbergs sju broar

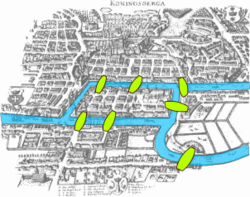
Allen är förtjust i kapitlet om kombinatorik med dess anknytande till grafteori och magiska kvadrater kompletterat med kartan från 1740 av Königsbergs sju broar, som i problemet ska korsar exakt en gång vardera. Han uppskattar Gullbergs redovisning av Fibonacci-, Lucas- och Pelnalföljder, och han tycker de två sidorna om Fermats stora sats håller ”exakt rätt nivå för dem som inte är specialiserade inom matematik samtidigt som framställningen givits en nivå av sofistikation".[4] Han uppskattade också kapitlet om sannolikhet. Han menar att efter att han visat boken för kollegor var han tvungen att hålla den gömd för att förhindra att den från att försvinna, och han föreslår att varje matematiklärare borde ges ett exemplar för att förbättra matematikundervisningen över hela Amerika. Han skriver att han finner den introducerande redovisningen användbar för ingenjörer, som bara sporadiskt använder sig av matematik, och han ger förslag på hur boken kan användas för universitetsstudenter. Han avslutar med att framföra att boken är ”storartad ... i varje avseende” (den omfattar 1100 sidor) och producerades över en period av 10 år, och han kallar den för ”ett jättekliv framåt för matematiken och för alla de som uppskattar detta ämne!”.[4]

Boken gavs positiva recensioner i Scientific American,[5] men fick mer reserverade utlåtanden i New Scientist.[6] Kevin Kelly har givit kommentaren att boken är en form av "orakel" genom att erbjuda svar på obskyra matematiska begrepp. Enligt hans uppfattning är boken full av "kvickheter och humor; man behöver uthållighet."[7]

Gullberg har givit kommentaren, "Till en början ville ingen ’riktig matematiker’ ta i min bok, och kanske var det lika tokigt av mig att skriva en bok om matematik, som det skulle vara för en matematiker att skriva en bok om kirurgi"[2]

Referenser

[redigera | redigera wikitext]
Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Jan Gullberg, 6 maj 2021.

Noter

[redigera | redigera wikitext]
  1. ^ ”Jan Gullberg, 62, Swedish Science Writer”. New York Times. 1998-06-18. https://www.nytimes.com/1998/06/18/world/jan-gullberg-62-swedish-science-writer.html?pagewanted=1. Läst 18 januari 2010. 
  2. ^ [a b c] ”Kirurgen Jan Gullberg skrev matematikens historia”. Läkartidningen 94 (45): sid. 4023–4025. 1997. http://ww2.lakartidningen.se/ltarkiv/1997/temp/pda16548.pdf. Läst 12 januari 2015.  Arkiverad 4 mars 2016 hämtat från the Wayback Machine. ”Arkiverade kopian”. Arkiverad från originalet den 4 mars 2016. https://web.archive.org/web/20160304025740/http://ww2.lakartidningen.se/ltarkiv/1997/temp/pda16548.pdf. Läst 1 juni 2021. 
  3. ^ Isdahl, Hans (2006). ”Skoleelever, matematikk og den hellige gral” (på norska). Skoleelever, matematikk og den hellige gral. Arkiverad från originalet den 2015-01-12. https://web.archive.org/web/20150112190754/http://matematikk.nordreisavgs.net/Privat/Jakten%20p%C3%A5%20den%20hellige%20gral.pdf.  Arkiverad 12 januari 2015 hämtat från the Wayback Machine.
  4. ^ [a b c d e f g] Allen, Arnold (January 1999). ”Reviews: Mathematics: From the Birth of Numbers. By Jan Gullberg”. The American Mathematical Monthly 106 (1): sid. 77–85. doi:10.2307/2589607. 
  5. ^ Albers, Donald J. (September 1998). ”Reviews”. Reviews. Scientific American. http://www.scientificamerican.com/article/mathematics-for-the-many/. Läst 18 januari 2010. 
  6. ^ Keith Devlin (1997-06-14). ”Those were the days”. Those were the days. New Scientist. https://www.newscientist.com/article/mg15420864.200-those-were-the-days.html. Läst 18 januari 2010. 
  7. ^ Kelly, Kevin. ”Mathematics: From the Birth of Numbers”. Mathematics: From the Birth of Numbers. http://kk.org/cooltools/archives/492. Läst 29 december 2014. 
Hämtad från ”https://sv.wikipedia.org/w/index.php?title=Mathematics:_From_the_Birth_of_Numbers&oldid=54049896”