Kvadratroten ur 3
Utseende
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2018-02) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
Kvadratroten ur 3 eller roten ur 3, är det positiva tal vars kvadrat är lika med 3. Talet skrivs som
Kvadratroten ur 3 är ett irrationellt tal. Talet är även känt som Theodorus konstant[1], efter Theodorus från Kyrene. Avrundat till tio decimaler är talet 1,7320508076 (talföljd A002194 i OEIS)
Bråket (1,7321...) är en approximation av kvadratroten ur 3.
Geometri
[redigera | redigera wikitext]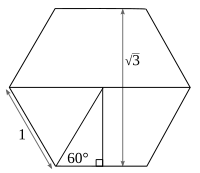
Höjden i en liksidig triangel med sidlängden 1 delar triangeln i två kongruenta rätvinkliga trianglar, vilka var och en har en katet med längden 1/2. Enligt Pythagoras sats är då höjden i den liksidiga triangeln lika med
Av detta fås att
Ytterligare geometriska egenskaper kopplade till :

- Kvadratroten ur 3 är avståndet mellan parallella sidor i en regelbunden sexhörning med sidlängden 1.
- Kvadratroten ur 3 är också lika med längden av rymddiagonalen i en enhetskub.
- En inskriven cirkel i en liksidig triangel med sidlängden kvadratroten ur tre har diametern 1.[2]
Externa länkar
[redigera | redigera wikitext] Wikimedia Commons har media som rör Kvadratroten ur 3.
Wikimedia Commons har media som rör Kvadratroten ur 3.- Bevis för att roten ur 3 är irrationellt (engelska)
- Theodorus konstant på Mathworld
Referenser
[redigera | redigera wikitext]- ^ Weisstein, Eric W.. ”Theodorus's Constant” (på engelska). mathworld.wolfram.com. https://mathworld.wolfram.com/TheodorussConstant.html. Läst 10 september 2021.
- ^ Den inskrivna cirkelns diameter är 2/3 av triangelns höjd och höjden är ju (Pythagoras sats - sidlängden, det vill säga hypotenusan i den rätvinkliga triangeln där triangelhöjden är en katet, är lika med och den andra kateten, den som inte är den liksidiga triangelns höjd, är lika med hälften av detta, eftersom den ju är en halv sida)
| |||||






