Kromatiskt tal

Kromatiskt tal är ett begrepp inom grafteorin i matematiken. Det kromatiska talet för en graf G, betecknat $\gamma (G)$, är det tal för en graf G som beskriver det minsta antalet färger som behövs för att färglägga grafen G. Vad som menas med att färglägga en graf kan tyckas oklart. I detta fallet kan man tänka sig ett antal hörn eller punkter som, på olika sätt, kombineras ihop med andra hörn. Detta görs genom att man drar linjer från ett hörn till ett annat. Principen går sedan ut på att om två hörn är i kontakt med varandra via en linje, får de inte ha samma färg. Med andra ord är det alltså hörnen man färgar och mellan hörnen dras linjer. Dessutom tillåts inte loopar, vilket betyder att en linje inte får återknytas till där den från början kom ifrån. Då det är omöjligt att tänka sig vilka färger hörnen i så fall skulle ha.

Klassiska grafer

K-graf	C-graf	S-graf	W-graf

Där $K_{n}$ är beteckningen för en så kallad komplett graf (K-graf), en graf där alla hörn är i kontakt med alla de andra hörnen, vilket också alltid gör att en komplett grafs antal hörn är samma som det kromatiska talet.

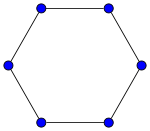
Bild nummer två är $C_{n}$ (C-graf), vilket står för cyklisk graf. Dessa är enkelt förklarade som cirklar, med andra ord ett hörn är i kontakt med nästa och det hörnet är i sin tur i kontakt med ytterligare en och så vidare till man når det första hörnet igen.

En stjärngraf (S-graf) betecknas med $S_{n}$ och består av ett hörn i mitten, vilket omges av ett antal hörn, alla dessa yttre hörn är i kontakt med mittenhörnet men inte med varandra.

$W_{n}$ står för wheel, alltså en hjulgraf (W-graf), som kan sägas vara en kombination av en stjärn- och en cirkelgraf. Det finns ett hörn i mitten som är i kontakt med alla de andra hörn som omger den. De hörn som omger mitten sitter alla ihop som i en cirkel. Detta kan ses i bilden.

Bakgrund

Det verkar först inte vara något större problem att färglägga dessa hörn med minimum antal färger, men att bestämma det kromatiska talet för en graf har faktiskt en NP (nondeterministic polynomial time )-svårighetsgrad. Det är därför vanligt att matematiker inte förväntar sig hitta algoritmer som kan lösa problemet.

Att det kromatiska talet är ett NP-problem betyder i princip, i det här fallet, att det inte finns något smidigt sätt att bestämma det kromatiska talet $\gamma (G)$ för en graf G. Och detta var just ett av Richard Karps 21 NP-problem, som han presenterade 1972.

Trots det har flera personer under lång tid kommit på exakta algoritmer för det kromatiska talet för en graf, men endast för speciella fall. Alla algoritmer som tagits fram genom åren har också det problemet att det kan ta fram ett tal som är tillräckligt många färger för att färga en graf, men att bevisa att det inte finns ett mindre tal tar betydligt längre tid. Det finns till exempel problem med 85 hörn som kan ta sekunder att lösa, men minuter om inte timmar för att bevisa att just det kromatiska talet är det minsta.

Olika lösningar på samma problem

4 hörn med 3 färger på 12 olika sätt

Till exempel på bilden till höger kan man se 12 olika sätt att med det kromatiska talet 3 rita en figur som består av 4 hörn. I detta fall varieras färgerna röd, grön och blå i de olika hörn utan att bryta mot förutsättningarna och samtidigt är det inte fler än 3 färger. Det kromatiska talet är alltså 3, men det finns 12 olika lösningar som alla är korrekta.

Formler

Där n är antalet hörn:

Graf	$N$	förutsättning	$N$	förutsättning
K-graf	n
C-graf, n>1	2	för jämna n	3	för udda n
S-graf	2
W-graf, n>2	3	för udda n	4	för jämna n

Här kan vi se att det finns exempel på grafer vars lösningar är lätta att beskriva och vi ser även att det kan spela roll ifall n är udda eller jämnt.

Här kan man se de fem första $K_{n}$-graferna (n=1,2,3,4,5).

Alla kromatiska tal är minst 1 och max n, där n är antalet hörn. Det ter sig förmodligen rätt naturligt, att när man får reda på att de grafer som bara har 1 färg är grafer helt utan linjer, alltså ett enda hörn. Grafer där varje hörn är av unik färg är $K_{n}$-graferna.

$1\leq \gamma (G)\leq n$

Om m är antal linjer mellan punkter så kan man se att 2 gånger alla linjer alltid är större eller lika med det kromatiska talet gånger det kromatiska talet minus 1. Är man osäker på om detta stämmer kan man testa detta med Petersens graf, som kan ses på bilden till höger.

Petersens graf

$\gamma (G)(\gamma (G)-1)\leq 2m$

Det är också fastställt att det kromatiska talet är åtminstone klicktalet.

$\gamma (G)\geq m\gamma (G)$

Höga klicktal ger alltså höga kromatiska tal, men motsatsen är inte nödvändigtvis sann. Det finns exempelvis grafer med höga kromatiska tal men med små klicktal.

Vidare är det alltid givet, att om man har att göra med planära grafer så kommer det kromatiska talet, för en sådan graf, alltid att vara högst 4. Det följer av fyrfärgssatsen.

Tillämpningar

Ett sätt att använda sig av kromatiskt tal i ett verkligt syfte är när man skapar kartor . Dessa kartor är färgade på så sätt att alla länder har en färg som är annorlunda jämfört med dess grannländer. Det är för att man ska tydligt kunna se skillnaderna på länderna och lätt ska kunna urskilja landgränser. Att använda sig av så få färger som möjligt (alltså det kromatiska talet) när man ritar kartan är oftast önskvärt. Flera länder har flera länder som de delar gräns med. Då kan man tänka sig att det är viktigt att få rätt kromatiskt tal. Se fyrfärgssatsen och femfärgssatsen.

Dessutom har sudoku koppling till färgning av grafer. Det kan man förstå genom att se att ingen siffra får befinna sig i samma kvadrat, i samma kolumn eller på samma rad som en likadan siffra.

Trivia

Ibland skrivs $\gamma (G)$ istället som $\chi (G)$, vilket också är benämningen för Eulerkarakteristik

Koppling till kromatiskt polynom

Det kromatiska talet för en graf $G$ med kromatiskt polynom $P_{G}(k)$ är det minsta positiva heltal som inte är en rot till $P_{G}(k)$.