Atwoodmaskin

Illustration av Atwoodmaskinen, 1905.

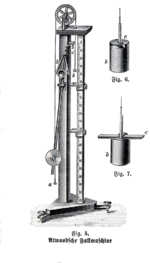
Atwoodmaskinen (eller Atwoods maskin) uppfanns 1784 av den engelske matematikern George Atwood som ett laboratorieexperiment för att verifiera lagarna för mekanisk rörelse med konstant acceleration. Atwoods maskin är en vanlig klassrumsdemonstration som används för att illustrera principer för klassisk mekanik.

Den idealiska Atwoodmaskinen består av två föremål av massa m₁ och m₂, anslutna med en oupplöslig masslös sträng över en idealisk masslös remskiva. Båda massorna upplever enhetlig acceleration. När m₁ = m₂ är maskinen i neutral jämvikt oavsett vikternas position.

Ekvation för konstant acceleration

Frikroppsdiagram av de två hängande massorna i Atwoodmaskinen. Vår teckenkonvention, avbildad av accelerationsvektorerna är att m₁ accelererar nedåt och att m₂ accelererar uppåt, vilket skulle vara fallet om m₁ > m₂

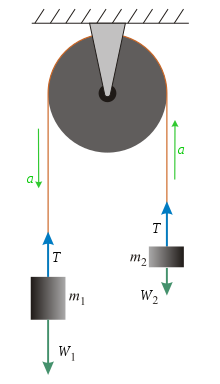
En ekvation för accelerationen kan härledas genom att analysera krafter. Förutsatt en masslös, oupplöslig sträng och en idealisk masslös remskiva är de enda krafter att tänka på: spänningskraft (T) och vikten av de två massorna (W₁ och W₂). För att hitta en acceleration, måste antas de krafter som påverkar varje enskild massa och använda Newtons andra lag (med en teckenkonvention av m₁ > m₂) för att härleda ett system med ekvationer för accelerationen (a).

Som teckenkonvention, antas att a är positiv när de är nedåtgående för $m_{1}$ och uppåt för $m_{2}$. Vikt av $m_{1}$ och $m_{2}$ är helt enkelt $W_{1}=m_{1}g$ och $W_{2}=m_{2}g$ respektive. Krafter som påverkar m₁: $\;m_{1}g-T=m_{1}a$ Krafter som påverkar m₂: $\;T-m_{2}g=m_{2}a$ och lägga till de två tidigare ekvationerna ger $\;m_{1}g-m_{2}g=m_{1}a+m_{2}a$, och den avslutande formeln för acceleration $a=g{m_{1}-m_{2} \over m_{1}+m_{2}}$ Atwoodmaskinen används ibland för att illustrera lagrangiansk metod för att härleda rörelseekvationer.

Ekvation för spänning

Det kan vara användbart att känna till en ekvation för spänningen i strängen. För att utvärdera spänning, ersätt ekvationen för acceleration i någon av de två kraftekvationerna. $a=g{m_{1}-m_{2} \over m_{1}+m_{2}}$

Till exempel kan du ersätta $m_{1}a=m_{1}g-T$, vilket resulterar i $T={2gm_{1}m_{2} \over m_{1}+m_{2}}={2g \over 1/m_{1}+1/m_{2}}$

Ekvation för en remskiva med tröghet och friktion

För mycket små masskillnader mellan m₁ and m₂ kan den roterande trögheten I hos remskivan av radie r inte försummas. Remskivans vinkelacceleration ges av halkfritt tillstånd: $\alpha ={a \over r},$ där alfa är vinkelaccelerationen. Nettovridmomentet är då:

$\tau _{\mathrm {net} }=\left(T_{1}-T_{2}\right)r-\tau _{\mathrm {friction} }=I\alpha$

Genom att tillämpa Newtons andra lag för de hängande massorna, och lösa ut T₁, T₂, and a, vi får:

Acceleration:

$a={{g(m_{1}-m_{2})-{\tau _{\mathrm {friction} } \over r}} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Spänning i strängsegmentet närmast m₁:

$T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}}+{{\tau _{\mathrm {friction} }} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Spänning i strängsegmentet närmast m₂:

$T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}}+{{\tau _{\mathrm {friction} }} \over {rg}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Kan lagerfriktion antas vara försumbar (men inte remskivans tröghet och inte dragkraften hos strängen på remskivans kant), förenklas dessa ekvationer som följande resultat:

Acceleration:

$a={{g(m_{1}-m_{2})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Spänning i strängsegmentet närmast m₁:

$T_{1}={{m_{1}g(2m_{2}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Spänning i strängsegmentet närmast m₂:

$T_{2}={{m_{2}g(2m_{1}+{{I} \over {r^{2}}})} \over {m_{1}+m_{2}+{{I} \over {r^{2}}}}}$

Praktisk implementering

Atwoods ursprungliga illustrationer visar huvudskivans axel som vilar på kanterna på ytterligare fyra hjul, för att minimera friktionskrafterna från lagren. Många historiska implementeringar av maskinen följer denna design.

En hiss med en motvikt approximerar en idealisk Atwoodmaskin och avlastar därmed körmotorn från belastningen av att hålla hisshytten - den måste övervinna endast viktskillnad och tröghet hos de två massorna. Samma princip används för bergbanor med två anslutna järnvägsvagnar på lutande spår och för hissarna på Eiffeltornet som balanserar varandra. Skidliftar är ett annat exempel, där gondolerna rör sig på ett slutet (kontinuerligt) remskivesystem upp och ner på berget. Skidliften liknar den motviktade hissen, men med en begränsningskraft som kabeln ger i vertikal dimension och därigenom uppnår arbete i både horisontella och vertikala dimensioner. Båthissar är en annan typ av motviktat hissystem som approximerar en Atwoodmaskin.

Referenser

Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Atwood machine, 4 maj 2019.

Externa länkar

• Wikimedia Commons har media som rör Atwoodmaskin.
  Bilder & media
• Professor Greenslade's account on the Atwood Machine
• Atwood's Machine by Enrique Zeleny, The Wolfram Demonstrations Project