Träd (datastruktur)

Ett enkelt exempel på ett osorterat träd. Den översta noden med värdet 2 är trädets rotnod.

Inom datavetenskap är träd en vanlig datastruktur som ordnar en mängd element hierarkiskt i ett riktat träd där varje nod bara kan ha en båge som leder in till noden. Rotnoden är den första noden i trädet, den enda nod som inte har några grenar som leder in. Från rotnoden finns det exakt en väg till varje annan nod i trädet.

Begrepp

Rotnoden, eller bara roten, är den första noden i trädet, den som inte har några grenar som leder in. De noder som man direkt kan ta sig till från en nod A kallas för dess barn eller direkta efterföljare. A är då förälder, eller direkt föregångare till sina barn. De noder som har samma förälder kallas för syskon.

En nod som saknar barn kallas löv eller slutnod och resten av noderna, de som har åtminstone ett barn, kallas inre noder. En nod kan maximalt ha en förälder, men antalet barn är godtyckligt och kallas för nodens grad. Trädets grad är den högsta graden hos någon av trädets noder men ofta avser detta istället den maximala grad (det maximala antalet barn) som en nod kan ha. Ett träd med grad 1 kallas för ett degenererat träd.

Anfäder till en nod är alla de noder som är föregångare till noden. Roten är anfader till alla andra noder i trädet. En nods avkomma är på motsvarande sätt alla de noder som har noden som anfader. En väg i ett träd är de grenar som passeras mellan en nod och dess anfader. Vägens längd (väglängd) är antalet grenar som den innehåller. För sökträd är medelväglängden särskilt intressant och den beräknas som summan av alla noders väglängd från roten delat med antalet noder.

Ett delträd är en nod inklusive dess avkomma. Den översta noden i delträdet är delträdets rotnod, man säger att delträdet är rotat i den noden. delträdet med rotnoden som rotnod är alltså hela trädet självt. delträd med någon annan nod som rot kallas ett äkta delträd. Ett träd består alltså av en nod vars barn är delträd.

En nod sägs ligga på nivå n i trädet, där n är väglängden från roten. Till exempel ligger rotnoden på nivå 0 och dess barn på nivå 1. En nods höjd är den längsta väglängden ner till ett löv. Alla löv har alltså höjden 0. Trädets höjd är lika med rotens höjd. Ett tomt träd har definitionsmässigt höjden 0.

Storleken på ett träd är antalet noder som trädet innehåller (inklusive rotnoden).

Ofta är ett träd orienterat vilket betyder att varje nods barn är ordnade. Om en nods grad är 2 (eller 3) kan man tala om vänsterbarn(, mittenbarn) och högerbarn. Högersyskon och vänstersyskon är alla de syskon som är ordnade till höger om respektive vänster om en nod. Ett närmaste syskon är endera det högersyskon eller det vänstersyskon som endast är ett steg ifrån.

Fullt träd

Ett fullt träd är ett träd där alla inre noder är fulla, det vill säga har maximalt antal barn (så många som trädets grad), och där alla löv ligger på samma nivå. Om en ny nod läggs till i ett fullt träd så ökar trädets höjd (med 1). Om dessa nya noder läggs till längst till vänster i den nya nivån (tätt) så kommer trädet att vara komplett, dvs utan hål.

Ett fullt träd med höjd h och grad g har storlek $(g^{h+1}-1)/(g-1)$. Antalet löv i trädet är $g^{h}$.

En fördel med kompletta träd är att de enkelt kan lagras i ett fält (kallas implicit representation) genom att numrera noderna uppifrån och ner, från vänster till höger. Det gäller att:

• Rotnoden har index 1 och den sista lövnoden har index n
• Om en nod har index i så har dess barn index $g*i-g+2+k$, där $k=0,1,...,g-1$
• Om en nod har index i så har dess förälder index $(i+g-2)/g$ (heltalsdivision).

Symboler

Ibland är det bara intressant att visa på ett träds övergripande struktur och inte exakt varje nod. För detta används ett antal symboler:

• 
  Godtyckligt träd
• 
  Komplett träd
• 
  Nod med två namngivna subträd

Vanliga operationer

Det finns flera vanliga operationer som görs på träd, några är:

• Uppräkning av alla element
• Uppräkning av alla element i en viss del av trädet
• Sökning
• Lägga till ett element på en viss position i trädet
• Borttagning av ett element (och dess nod)
• Borttagning av ett delträd (ansning)
• Lägga till ett delträd (ympning)

Trädtraversering

Traverseringsordning på djupet först i ett binärt sökträd. Varje nod besöks tre gånger. När turen kommer till noden B och dess underlydande delträd, kan de undersökas i olika ordning:

  Preorder, B före delträden: B-A-D.

  Inorder, B mellan delträden: A-B-D.

  Postorder, B efter delträden: A-D-B.

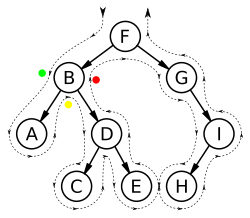
Traversering av ett träd innebär att man besöker trädets alla noder på ett systematiskt sätt. Dessa sätt kan delas in i två huvudkategorier: djupet först eller bredden först.

Djupet först traversering kan göras i preorder, inorder eller postorder, vilket betyder att en nod evalueras innan, mellan eller efter att dess barn evaluerats.

Uttrycksträd

Ett uttrycksträd representerar ett uttryck. Operatorer återfinns i inre noder och värden i lövnoder. Eftersom träd är hierarkiska precis som uttryck avspeglar de entydigt uttryckens beräkningsordning utan att parenteser behöver användas.

Om man traverserar ett uttrycksträd inorder får man det vanliga infix-uttrycket. Preorder och postorder ger polsk notation respektive omvänd polsk notation. Av dessa tre är det endast infix-uttrycket som kan behöva parenteser för att entydigt beskriva beräkningsordningen.

Sökträd

Om man låter all data i trädet vara systematiskt ordnat kan man erhålla strukturer som är effektiva för att söka i. De två huvudkategorierna av sökträd är binära sökträd och mångförgrenade sökträd.

Referenser

• ”Träd | IDG:s ordlista”. IT-ord. https://it-ord.idg.se/ord/trad-2/. Läst 9 september 2023.