Sinussatsen

Sinussatsen är inom trigonometrin en sats om trianglar. För en triangel med sidlängderna a, b och c, och med de motstående vinklarna betecknade med α, β och γ enligt

så gäller enligt sinussatsen att

${\frac {\sin \alpha }{a}}={\frac {\sin \beta }{b}}={\frac {\sin \gamma }{c}}$

Det tvetydiga fallet

Vid tillämpning av sinussatsen existerar ett tvetydigt fall där två olika trianglar svarar mot den givna beskrivningen om det enda som är känt om triangeln är vinkeln A och sidorna a och b.

Det finns då två möjliga värden för vinkeln B beroende på vinkeln C:

$B=\arcsin {b\sin A \over a}$

eller

$B=180^{\circ }-\arcsin {b\sin A \over a}$

Härledning

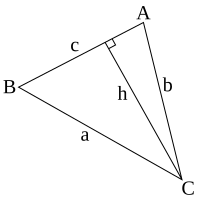
Antag en triangel med sidorna a, b och c och med de motstående vinklarna A, B och C. En linje med längden h och vinkelrät mot sidan c är dragen från hörnet C till motstående sida c eller sidan c:s förlängning.

Då är

$\sin A={\frac {h}{b}}$

och

$\;\sin B={\frac {h}{a}}$

Vilket är ekvivalent med

$h=b\,\sin A=a\,\sin B$

och

${\frac {\sin A}{a}}={\frac {\sin B}{b}}$

Om linjen dras mellan vinkeln A och sidan a och samma procedur upprepas blir resultatet

${\frac {\sin B}{b}}={\frac {\sin C}{c}}$

Se även

• Areasatsen
• Cosinussatsen
• Tangenssatsen