Signalförstärkning
Elektrisk förstärkning kallas en aktiv, linjär ökning av en signal så att en högre effekt erhålls. Detta uppträder när man skickar in en signal på en förstärkare och får en större signal på utgången. En vanlig standardkomponent som används vid förstärkning är operationsförstärkaren (OP) men även diskreta transistorer används, ävensom andra metoder. Spänningsökning med transformator kallas inte förstärkning, eftersom strömmen minskar, och effekten de facto minskas.
Operationsförstärkaren
[redigera | redigera wikitext]
Det finns två typer av förstärkning. Dels råförstärkningen som operationsförstärkaren har vid i öppet tillstånd, utan motkoppling, dels den motkopplade förstärkningen i datablad ofta betecknad Av som kan utläsas "voltage amplification".
En förstärkare förstärker inte alltid elektrisk spänning utan kan förstärka både strömstyrka och en kombination av ström och spänning. Det allra vanligaste i fallet småsignal är dock att förstärkaren förstärker spänning även om utgångsimpedansen ofta är mycket lägre än den drivande impedansen så att man på detta sätt även får en strömförstärkning.
När det gäller operationsförstärkarens spänningsförstärkning, finns det två grundkopplingar enligt figur. Den ena är den "icke-inverterande förstärkarkopplingen", den andra är den "inverterande förstärkarkopplingen".
I framställningen nedan förutsätts närmast ideala operationsförstärkare, med försumbart strömbehov på ingångarna, försumbar olinjäritet, extremt hög råförstärkning och inget behov av frekvenskompensering eller offset. En ingång är positiv (icke-inverterande) och en negativ (inverterande), kopplade som differentialförstärkare för spänning, med en positiv utgång. Många verkliga förstärkare har dock annorlunda egenskaper.
Icke-inverterande koppling
[redigera | redigera wikitext]I denna koppling kopplas en del av utsignalen tillbaka till minus-ingången. Denna signal får ingångsspänningen att minska och vi har då en negativ återkoppling. Spänningen in på själva operationsförstärkaren kan tecknas:
där
Samtidigt har vi
Efter eliminering av e och algebraisk utveckling har vi slutligen
och om
så blir förstärkningen
och alltså enbart beroende av resistanserna R1 och R2. Eftersom råförstärkningen, F, för många standardförstärkare är i storleksordningen 100 dB eller 100 000 så blir förstärkningen i alla praktiska fall när nog exakt 1/β.
En spänningsföljare kan skapas genom att utesluta R1, och låta R2 vara hur litet som helst. Denna har egenskapen att replikera inspänningen och kunna driva en utgångslast med stark ström utan att belasta signalkällan.
Inverterande koppling
[redigera | redigera wikitext]Man kan på liknande sätt visa att förstärkningen för den inverterande kopplingen blir:
Alternativt kan man se kopplingen som sådan att plusingången är jordad och att e motsvarar en extremt liten potential då råförstärkningen, F, normalt är så ofantligt stor. Impedansen mellan plus och minus är samtidigt normalt mycket stor (se arkitekturen nedan). Vi har med andra ord fått en virtuell jord.
När vi konstaterat detta kan vi titta på kopplingen med andra ögon. Strömmen in, Iin, blir
Och denna ström måste även gå genom R2 då ingen ström kan gå in på den högimpediva minusingången. Utgången måste alltså gå negativ och eftersom det är samma ström är utspänningen proportionell mot de båda motstånden enligt inledande formel ovan.
Operationsförstärkarens frekvensberoende
[redigera | redigera wikitext]Ovanstående resonemang håller endast då frekvensen är låg eller då återkopplingen är stor. I själva verket avtar råförstärkningen både tidigt och snabbt med frekvensen. Vanligast är att överföringsfunktionens Laplacetransform har polen som en enkelpol runt något tiotal hertz. Råförstärkningen avtar då med 20 dB/dekad men operationsförstärkaren kan ha fler poler varvid råförstärkningen avtar ännu snabbare. Så länge som antalet poler är mindre än tre så är förstärkaren stabil vid alla grader av återkoppling. Vissa operationsförstärkare måste dock frekvenskompenseras med en kondensator för att kunna användas vid 0 dB förstärkning (läs som spänningsföljare dvs med R1 i den icke-inverterade kopplingen borttagen). Viss frekvenskompensering görs i förstärkarkopplingen, annan på speciella anslutningar som tillverkaren har förberett för ändamålet.
Råförstärkningen är alltså alltid beroende av frekvensen. Man har infört en beteckning kallad GBW eller Gain Bandwidth Product, förstärkningsbandbreddsprodukt. Detta tal motsvarar operationsförstärkarens bandbredd vid 0 dB förstärkning. För att få bandbredden vid vald förstärkning delar man helt enkelt GBW med den förstärkning man vill ha och får då en lägstauppskattning av bandbredden för den förstärkningen. Detta gäller oavsett hur många poler OP:n har.
Eftersom råförstärkningen är så stor så behöver man normalt inte bry sig om OP:ns frekvensberoende. Det är främst vid kombinationen stor förstärkning och hög frekvens som speciella begränsningar uppkommer. Detta gäller exempelvis vid förstärkning av små signaler från pick-up'er eller dynamiska mikrofoner. I sådana fall kan hög förstärkning åstadkommas med kaskadkoppling av förstärkare.
Konstruktionsexempel
[redigera | redigera wikitext]Antag att vi har en standard operationsförstärkare med en maxförstärkning på 100 dB och en enkelpol eller bandbredd på 10 Hz. En sådan förstärkare har då överföringsfunktionen
med absolutbeloppet
Säg sedan att vi önskar förstärka 40 dB eller 100 gånger för vår mikrofon. Vi har då
Eftersom råförstärkningen faller 20 dB/dekad och således når 0 dB fem dekader efter enkelpolen har vi
- eller 1 MHz.
Enligt resonemanget ovan hamnar vi således på en bandbredd på endast
vid 100 gångers förstärkning.
Märk dock att vi har ökat den effektiva bandbredden 1 000 gånger tack vare motkopplingen.
Offset
[redigera | redigera wikitext]
Trots att ingångstransistorerna tillverkas på samma chip blir de inte helt lika. Även vid exakt samma inspänning blir det ofta en intern differens som förstärks enligt förstärkningsfaktorn. Denna avvikelse kallas offset är ofta i storleksordningen 5 mV.
Det finns ett antal sätt att justera offset. Bilden till höger visar två generella sätt. Vissa operationsförstärkare har dock separata ingångar för offset-justering. Dessutom kommer den motkopplade förstärkningen, Av, att påverkas något i den icke-inverterande kopplingen (men inte alls i den inverterande kopplingen). Men då R är så litet (i storleksordningen 100 Ω) i jämförelse med övriga komponenter kan påverkan ofta försummas.
Offset behöver alltså justeras vid hög förstärkningsfaktor eller där hög precision fordras. Generellt sett är problemet störst vid DC, eftersom ett förstärkarstegs offset inte har samma betydelse vid AC-bruk, lite beroende på hur stegen är kopplade.
Operationsförstärkarens arkitektur och egenskaper
[redigera | redigera wikitext]
Bilden visar en fullt möjlig realisering av en operationsförstärkare. Skillnaden mellan denna och kommersiella varianter är främst extra förstärkningssteg, strömbegränsning och antalet motstånd.
CMRR
[redigera | redigera wikitext]CMRR står för Common Mode Rejection Ratio. Det avser mått på en olinjäritet som kan göra att en viss spänningsdifferens mellan ingångarna kan resultera i olika utsignal vid olika signalspänning, fast den skulle vara identisk. Den beräknas med en common-mode signal som är en gemensam signal, och en skillnadssignal (differentiell signal), och denna kvot anges av tillverkaren som CMRR.[1] Common-mode-signalen kan ses som en störningskälla som skapar distorsion av den differentiella signalen, "meddelandesignalen", som är den signal man vill förstärka. Detta är aktuellt i en miljö med störningar som påverkar bägge insignalsledningarna. Om man använder en instrumentförstärkare kan man eliminera common-mode delen av signalen och förstärka den differentiella signalen, det vill säga spänningsskillnaden mellan två punkter.[2]
CMRR kan räknas ut på följande sätt (se figur):
Vid drain på T1 eller T2 har vi (se signalförstärkning medels FET-transistor nedan)
Detta för att T3's impedans inte märks för differentiella signaler. För gemensamma signaler fås en förstärkning:
- där ro är strömspegelns dvs T3's utgångsimpedans.
CMRR definieras som kvoten mellan förstärkning av skillnadssignal (Avdm/2) och gemensam signal (Avcm) enligt:
Där ro kan vara väldigt stor. Speciellt om emitterresistans används. Utan emitterresistans, såsom i figur, blir ro endast av storleksordningen 100 kΩ dvs transistor T3's utgångsimpedans. Det kan dock visas att även med ett måttligt emittermotstånd kan effektiv impedans vara av storleksordningen MΩ (megaohm).
PSRR
[redigera | redigera wikitext]PSRR står för Power Supply Rejection Ratio. I förstärkaren ovan används en strömspegel (T3 och T4). När matningsspänningen (Vcc-Vss) ökar kommer strömmen genom R att öka. Detta får till följd att strömspegelströmmen, Ic, ökar. När Ic ökar sjunker potentialen hos T1 och T2's drain. Detta får till följd att det finns en inbyggd automatisk korrigering för förändringar i matningsspänning. En störning i matningsspänningen innebär dessutom en "common-störning" (se Vcm i figur) dvs båda de differentiellt kopplade ingångstransistorerna (T1 och T2) kommer att få en lika stor påverkan i bias. P.g.a. detta är PSRR av samma storleksordning som CMRR, dvs typiskt 100dB för kommersiella operationsförstärkare.
Strömspegel
[redigera | redigera wikitext]Det som ovan har kallats strömspegel (eng. Current Mirror) utgörs av transistorerna T3 och T4. Om dessa är lika är strömmen genom R lika med
Strömmen genom R kan sedan sättas till:
Denna ström är mer eller mindre exakt den som flyter genom T3 då Ib är lika för de båda transistorerna och β (hFE) för småsignaltransistorer är av storleksordningen 100.
Nivåskiftare
[redigera | redigera wikitext]Vz är en zenerdiod. De kan användas i nivåskiftare. Dess funktion är att minska spänningen utan förluster. Detta för att T1 och T2 behöver en viss spänning mellan drain och source för att ha en lämplig arbetspunkt men detta innebär samtidigt att drainspänningen måste hållas relativt hög då gate alltid dras till jord. I ovanstående fall finns tre bas-emitter-spänningsfall innan Vz behöver beräknas. Dessa spänningsfall kommer av drivtransistorn T5 för zenerdioden samt två i darlingtontransistorn T6 före utgången. Utgången bör hålla 0 volt vid noll volts ingående spänningsdifferens.
Darlingtontransistor
[redigera | redigera wikitext]T6 är en kopplad som darlingtontransistor. En darlingtonkopplad transistor består av ytterligare minst en transistor i en seriekoppling som ökar strömförstärkningsfaktorn till produkten av de ingående transistorernas förstärkningar. Dessa transistorer kan vara lika eller olika, NPN eller PNP i olika kombinationer. Om β (hFE) är lika blir resulterande strömförstärkningen
och nästan exakt β för respektive transistor mutiplicerat.
Slew Rate
[redigera | redigera wikitext]Slew Rate, SR, är mått på hur snabbt utspänningen kan ändras, alltså brantheten i V/s. Även om inspänningen växlar "oändligt snabbt", behöver utgången tid på sig för spänningsändringen, på grund av inbyggda begränsningar. Denna karaktäristik brukar i tillverkarens datablad anges i V/μs och är intimt förknippad med bandbredden hos operationsförstärkaren. Man kan visa att den så kallade Power Bandwidth, fp, är:
där Eop är max utgångssving hos operationsförstärkaren. Detta är alltså den maximala frekvens för en sinussignal som kan återges med maximal amplitud och 1 % distorsion.
En snarlik relation till SR har småsignalsbandbredden, fo, enligt
där tr är stigtiden hos utgångssignalen (exciterad av en snabbare ingångspuls).
För formens skull kan vi slutligen definiera SR som
det vill säga derivatan av spänningen med avseende på tiden.
Entransistorförstärkare
[redigera | redigera wikitext]
Bilden visar en spänningsförstärkare som bara består av en enda transistor, en förstärkartyp med gemensam emitter. Dess funktion är alltså att förstärka inkommande spänning (Uin) ett antal gånger för att generera utspänningen (Uut). Kvoten Uut/Uin kallas sedan dess spänningsförstärkning eller i normala fall bara förstärkning.
Konstruktionsexempel
[redigera | redigera wikitext]Transistorn T1 har en strömförstärkningsfaktor β eller hFE vanligen överskridande 100 gånger. Denna strömförstärkningsfaktor definieras som kvoten mellan kollektorströmmen, Ic, och basströmmen, Ib. För en viss Ic räcker det med Ib som är Ic/hFE, alltså ungefär en hundradel.
Om vi nu betänker detta så innebär det att om man ser till så att strömmen genom Rb1 och Rb2 (grovt räknat) är säg, Ic/10 (så klarar vi oss nästan alltid då Hfe ≫ 100 normalt) så kommer vi inte att behöva bekymra oss om den lilla basström som annars skulle sänka baspotentialen något utan kan säga att potentialen vid basen är:
När nu baspotentialen är bestämd kan vi bestämma emitterströmmen, Ie, (då ju Ie = Ib + Ic men Ic ≫ Ib varför Ie ≈ Ic) eftersom vi alltid har (för kiseltransistorer) ett bas-emitter-spänningsfall motsvarande crika 0,7 V. Om man tar detta i beräkning så får man, mycket lite förenklat, en kollektorström, Ic, motsvarande baspotentialen, Vb, minus Vbe (0,7 V) delat med emittermotståndet, Re.
Förutom detta är det lämpligt att transistorn, T1, och kollektormotståndet, Rc, delar på övrig spänning (så att utgången kan svinga lika mycket positivt som negativt). Men som vi ska se senare innebär detta i de flesta CE-sammanhang (med hyfsad förstärkning) att spänningen över Re mer eller mindre kan försummas.
Vi har alltså att:
och sedan
Eftersom samma ström, enligt vår definition, flyter genom Re som genom Rc så förstås nästan intuitivt att förstärkningen blir (se nedan):
Av erfarenhet så lär man sig sen sätta en biasnivå (Vb) där det finns "plats" (läs spänningsutrymme) för godtycklig, alltså totalt transistoroberoende, förtärkning. Trixet är alltså inte att välja motstånd eller ström utan trixet är att välja spänningsmässig arbetspunkt.
Nackdelen med denna entransistorförstärkare är att den har hög utgångsimpedans (i praktiken Rc, se nedan) varför det inte går att driva till exempel hörlurar med den. Genom att koppla en darlingtontransistor som emitterföljare (se nedan) på utgången kan man dock få ner både belastningen på entransistorförstärkaren och dess utgångsimpedans så att det blir fullt möjligt att driva en hörlur med endast "två" transistorer per kanal.
Signalförstärkning medels FET-transistor
[redigera | redigera wikitext]
Signalförstärkning kan göras med hjälp av en FET-transistor. Se vidstående figur.
Kirchhoffs spänningslag säger att
och
vilket ger
Vo1 och Vo2 tas från drain (D) till jord respektive från source (S) till jord. Således är:
och
Spänningsförstärkningen vid Vo2 blir (GD=Gemensam Drain eller sourceföljare)
och spänningsförstärkningen vid Vo1 blir (GS=Gemensam Source)
och kortslutningsströmmen vid samma nod blir
då blir
På samma sätt blir
På anoden ser man alltså i GS-fallet drain-resistansen, rd, summerat med den förstärkta sourceresistansen (u+1)Rs.
På katoden ser man på samma sätt i GD-fallet drain-resistansen, rd, summerat med den externa drainresistansen, Rd, med dess summa dämpad u+1 ggr.
Ovanstående ekvationer är lika giltiga för rörkopplingar.
Signalförstärkning medels BJT-transistor
[redigera | redigera wikitext]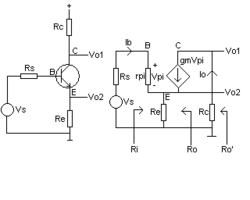
Signalförstärkning kan göras med en BJT-transistor (bipolär transistor). Se vidstående figur.
Kirchhoffs spänningslag säger att
och potentialen på basen blir
Strömförstärkningen blir
Ingångsimpedansen Ri blir:
Nu kan vi uttrycka källan Vs på ett annat sätt:
Även baspotentialen kan förenklas till:
GE(Gemensam Emitter)-förstärkningen blir:
GE-förstärkningen kan också skrivas:
Ro' är i GE-fallet lika med Rc då vi har förenklat modellen något (ro=oändlig).
GK(Gemensam Kollektor)-förstärkningen blir:
GK-förstärkningen kallas emitterföljare och kan förenklas till:
Ro' kan i GK-fallet kalkyleras på följande sätt:
I kortslutningsfallet är Re=0:
Kortslutningsströmmen Isc kan beräknas enligt
Utgångsimpedansen blir
Vilket efter en stund inses vara lika med
där
eller
Emitterföljarens utgångsimpedans är alltså normalt sett beroende av källimpedansen Rs men väldigt nära 1/gm i praktiska fall. Transkonduktansen för bipolära transistorer (BJT:s) är
(mA/mV)
där är kollektorströmmen vid vila.
Transkonduktansen gm är alltså ganska stor för BJT:s. Vid 2,5 mA är den till exempel 0,1 S.
Signalförstärkning medels biaserad BJT-transistor
[redigera | redigera wikitext]
Ovanstående nyckelekvationer repeteras här på grund av lämplighet.
I figuren har vi även infört
Kirchhoffs spänningslag säger att
Eftersom IinRs kan förkortas bort får vi efter lite algebraiskt trixande
Strömförstärkningen blir
Om vi inför
kan uttrycket förenklas till
vilket rätt intuitivt kan förstås då det ju går en del av inkommande ström genom Rp förutom till basen. Alltså blir effektiv Beta alltid något mindre vid användande av basmotstånd.
Baspotentialen är
detta ger
och inresistansen blir då
vilket helt enkelt är parallellkombinationen av och Rp. Enligt ekvation (2) hade vi inströmmen som funktion av basströmmen, denna ekvation ger nu naturligtvis även
Ekvation (1) ger samtidigt
och då blir spänningsförstärkningen
och om Rs är noll kollapsar ekvationen till
vilket fascinerande nog är samma uttryck som för en BJT utan basmotstånd!
Om man slutligen definierar
Kan vi på ett mycket enkelt sätt skriva (3) som
Här kan noteras att nedanstående upplaga av Physics Handbook får ifrågasättas. För att (3) ska gälla och inte kollapsa till (4) gäller att Rs måste vara skild från noll (vilket den alltid är i praktiken). Detta inses då en fullkomligt ideal signalkälla (Rs=0) gör att det kan gå hur mycket ström som helst genom Rp utan att baspotentialen och därmed spänningsförstärkningen påverkas.
Detta spelar faktiskt roll om man till exempel önskar förstärka en högimpediv pick-up's signal med ett par vanliga BJT:er (bipolära transistorer) i kaskad och inte m.h.a. differentialförstärkare modell operationsförstärkare.
Se även
[redigera | redigera wikitext]Källor
[redigera | redigera wikitext]- Millman Jacob, Grabel Arvin, Microelectronics, Second Edition, 1988, Singapore
- Walter G. Jung, IC Op-Amp Cookbook, Third Edition, 1988, USA
- Carl Nordling, Jonny Österman and Studentlitteratur, Physics Handbook, Fourth Edition, 1987, Lund (F-4.4)
Referenser
[redigera | redigera wikitext]- ^ ”Common-Mode Rejection Ratio”. Räknehjälp - Elektronik för E. LTH.se. http://www.eit.lth.se/fileadmin/eit/home/dry.jln/Elektronik/handout1.pdf. Läst 1 oktober 2012.
- ^ ”Instrumentförstärkare”. Instrumentförstärkare. Arkiverad från originalet den 5 mars 2016. https://web.archive.org/web/20160305001927/http://www8.tfe.umu.se/courses/elektro/elmat1/v36_01_da/semG1/op.html. Läst 1 oktober 2012.



































![{\displaystyle Ro1'={\frac {Vo1}{I_{sc}}}=Rd//[r_{d}+R_{s}(\mu +1)]=(R_{s}=0)=R_{d}//r_{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c4a93329f5a47b6fb05e961eaf107898a514976)






































