Växelström

Periodisk växelström

Icke-periodisk växelström. Skulle kunna vara utsignalen från en mikrofon

Växelström, AC (eng. alternating current), är en elektrisk ström vars riktning växlar. Om strömmen vid en viss tidpunkt har en viss riktning kommer den vid en senare tidpunkt att ha motsatt riktning. Kraftverksproducerade växelströmmar och växelspänningar är periodiska och följer med tämligen stor noggrannhet en sinuskurva.

Framförallt är det möjligheten att enkelt och med små förluster transformera växelströmmen som gjort den till standard i de allmänna elnäten. Kraftöverföring över stora avstånd kan ske med högspänningsledningar vilka ger relativt små överföringsförluster, samtidigt som det är enkelt att åstadkomma anpassade spänningar för anslutna apparater och maskiner.

Radiosignaler, och TV-signaler som transporteras med elledningar är också exempel på växelström. Dessa typer av växelströmmar bär information genom modulering av AC-signalen (bärvågen), såsom ljud (audio) eller bilder (video). Dessa strömmar använder mycket högre frekvenser än de som används vid kraftöverföring. Om två olika frekvenser av växelström passerar genom en olinjärt komponent bildas nya frekvenser. Se mixer

Sinusformad växelström

Sinusformad växelstorhet

Sinuskomponenter av olika frekvens, ger en periodisk, icke-sinusformad funktion när de adderas

Av grundläggande betydelse är växelströmmar och växelspänningar som varierar sinusformigt med tiden. En allmän sinusformad växelstorhet kan skrivas

$a={\hat {a}}\sin(\omega t+\alpha )=A{\sqrt {2}}\sin(\omega t+\alpha )\,$

där

$a$	ögonblicksvärdet (momentanvärdet)
${\hat {a}}$	toppvärdet (maximivärdet, amplituden)
$\omega \,$	vinkelfrekvensen i radianer per sekund
$t$	tiden
$\alpha$	fasvinkeln
$A$	effektivvärdet

Tiden för en period, perioden eller periodtiden är

$T={\frac {2\pi }{\omega }}\,$

Antalet perioder per sekund, periodtalet eller frekvensen

$f={\frac {\omega }{2\pi }}={\frac {1}{T}}\,$

Enheten för frekvens är hertz (Hz).

För en sinusformad växelstorhet är

$A={\frac {\hat {a}}{\sqrt {2}}}$

Elektrisk tvåpol

Tvåpol

En tvåpol är en elektrisk krets med endast två anslutningspunkter (se Thévenins teorem, Nortons teorem).

Allmän passiv tvåpol

En passiv tvåpol (som inte innehåller transistorer, ström/spänningskällor eller andra "aktiva" element) kan abstraheras till en tvåpol med konstanta egenskaper. Beroende på dess uppbyggnad kommer tvåpolen att ha en kapacitiv eller induktiv karaktär, vilket bestämmer dess fasförskjutande förmåga och hur den behandlar mottagen/avgiven effekt.

För en induktiv eller kapacitiv tvåpol, ger periodiska växelströmmar upphov till en energilagrande förmåga. Energi lagras i elektromagnetiska fält (laddningskonfigurationer) under en del av växelströmsperioden. Denna effektdel, som kallas reaktiv effekt, kommer att sändas tillbaka till växeleffektkällan under en annan del av växelströmsperioden. De ledningsströmmar som ger upphov till reaktiv effekt innebär kostnader (ledningsförluster) för både förbrukare och producenter. Därför används olika tekniker för faskompensering som kan implementeras på både förbrukar- och producentsidan.

Förhållandet mellan växelspänning och växelström för en tvåpol är enligt Ohms lag

$\ U=Z\cdot I$

där Z är kretsens impedans, vilken i det allmänna fallet är sammansatt av resistans och reaktans.

Fasförskjutning

Induktiv fasförskjutning. Spänningen ligger före strömmen

Kapacitiv fasförskjutning. Strömmen ligger före spänningen

Visardiagram för tre seriekopplade impedanser med resistans, induktans och kapacitans (R är riktfas)

Induktiva och kapacitiva kretsar orsakar fasförskjutning mellan spänning och ström.

Induktiv fasförskjutning (ideal induktor)

Om växelström leds genom en förlustfri spole uppstår en spänning över spolen som är proportionell mot den magnetiska flödesändringen per tidsenhet:

$u={d\Phi \over dt}=L{di \over dt}$

Om växelströmmen varierar enligt sin(ωt) blir spänningen över kretsen

$u=L{\frac {d}{dt}}\sin \omega t=\omega L\cos \omega t=\omega L\sin \left(\omega t+{\frac {\pi }{2}}\right)\,$

och spänningen kan således sägas ligga 90° före strömmen.

Kapacitiv fasförskjutning (ideal kondensator)

En växelspänning över en kondensator orsakar en upp- och urladdnining av kondensatorn enligt

$i={\frac {dQ}{dt}}=C\ {\frac {du}{dt}}$

Om spänningen varierar som sin(ωt) blir strömmen genom kondensatorn

$i=C{\frac {d}{dt}}\sin \omega t=\omega C\cos \omega t=\omega C\sin \left(\omega t+{\frac {\pi }{2}}\right)$

det vill säga, strömmen kan anses ligga 90° före spänningen.

Kretsar med förluster

Om tvåpolen har förluster (resistiva förluster, värmeutveckling) kommer fasförskjutningarna att variera mellan 0 och ±90°.

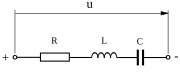
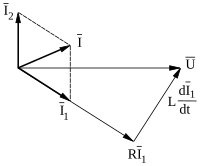
Till exempel kan den resulterande fasförskjutningen för en seriekoppling av tre komponenter med resistans, induktans respektive kapacitans, beräknas som (visaren för R används som riktfas)

$\theta =\arctan {\frac {\omega {\text{L}}-{\cfrac {1}{\omega {\text{C}}}}}{\text{R}}}$

enligt visardiagrammet till höger.

Effekt i växelströmskretsar

Figur 1: Motoriskt referensval, effekt tillförs tvåpolen

Den utvecklade momentan- och medeleffekten för en växelströmskrets. Strömmen och spänningen är inbördes fasförskjutna. Notera att effekten kan vara både positiv (mottagen) och negativ (avgiven)

Sinusformade spänningar och strömmar

Vid behandling av effektutveckling i växelströmskretsar är det viktigt att skilja mellan momentaneffekt och medeleffekt.

Momentaneffekten är definitionsmässigt p = ui, det vill säga produkten av spänningens och strömmens momentanvärden (ögonblicksvärden). I det allmänna fallet varierar både u och i med tiden och således även p. För momentaneffekten är det också nödvändigt att ange om p står för mottagen eller avgiven effekt.

Tvåpolen i figur 1 har motoriskt referensval, vilket innebär att momentaneffekten referensmässigt står för mottagen effekt sett från tvåpolen. Om effekten är mottagen eller avgiven anges av p:s tecken.

Spänning och ström antas vara sinusformade:

$\ u={\hat {u}}\sin(\omega t+\varphi _{u})$

$\ i={\hat {\imath }}\sin(\omega t+\varphi _{i})$

Den mottagna effekten kan då skrivas

$\ p=ui={\hat {u}}{\hat {\imath }}\sin(\omega t+\varphi _{u})\sin(\omega t+\varphi _{i})$

vilket kan skrivas om till

$\ p=UI\cos(\varphi _{u}-\varphi _{i})-UI\cos(2\omega t+\varphi _{u}+\varphi _{i})$

där U är spänningens effektivvärde och I är strömmens effektivvärde. Om φ definieras som

$\ \varphi =\varphi _{u}-\varphi _{i}$

det vill säga, som faskillnaden mellan spänning och ström, kan effekten skrivas som

$\ p=UI\cos \varphi -UI\cos(2\omega t+\varphi _{u}+\varphi _{i})$

Den momentana effekten kan således anses bestå av två delar:

• En konstant del

$UI\cos \varphi$

som om φ < 90° (motsvarar en passiv tvåpol) alltid är ≥ 0

• En med dubbla frekvensen varierande del

$UI\cos(2\omega t+\varphi _{u}+\varphi _{i})$

Aktiv effekt

Visardiagram över aktiv och reaktiv effekt. $\ \varphi$ är fasvinkeln mellan spänning och ström. Den reaktiva effektens tecken beror av tecknet för $\ \varphi$
(P) - Aktiv effekt
(Q) - Reaktiv effekt
(S) - Skenbar effekt

Den av tvåpolen förbrukade effekten (medeleffekten) är den konstanta delen

$\ P=UI\cos \varphi$

vilken också kallas aktiv effekt och har enheten watt.

Reaktiv effekt

Om

$\ |\cos \varphi |<1$,

det vill säga om ström och spänning är fasförskjutna, förekommer reaktiv effekt, vilken har enheten voltampere reaktiv (var).

Över en period är summan av de reaktiva effektbidragen noll. Den reaktiva effekten mottages och avges endast och förbrukas således inte av tvåpolen. Den reaktiva effekten är

$\ Q=UI\sin \varphi$

Referensmässigt räknas effekten som positiv om Q är av induktiv karaktär.

Skenbar effekt

Skenbar effekt är produkten av strömmens och spänningens effektivvärden:

$\ S=UI$

Skenbar effekt har enheten voltampere (VA) och är den effekt som anges som förbrukning för produkter som kopplas till elnätet. Vi ser av visardiagrammet att den skenbara effektens belopp ges av

$S={\Big |}{\sqrt {P^{2}+Q^{2}}}{\Big |}$

Den skenbara effektens tecken bestäms av tecknet för den reaktiva effekten.

Effektfaktor

Faktorn $\ \cos \varphi$ är av stor betydelse vid sinusformigt varierande spänning och ström och benämns effektfaktorn. Dess värde beror på tvåpolens uppbyggnad eftersom denna är avgörande för φ:s belopp och tecken. Effektfaktorn kan också skrivas som

$\ \cos \varphi ={P \over UI}={P \over S}$

Effekt vid icke sinusformade spänningar och strömmar

Medeleffekten definieras som

$P={1 \over t_{2}-t_{1}}\int _{t_{1}}^{t_{2}}ui\,dt$

Tvåpolens spänning och ström antas vara uppdelade i fourierkomponenter enligt

$\ u=U_{0}+U_{1}{\sqrt {2}}\sin(\omega t+\varphi _{11})+U_{2}{\sqrt {2}}\sin(2\omega t+\varphi _{12})+\dots$

$\ i=I_{0}+I_{1}{\sqrt {2}}\sin(\omega t+\varphi _{21})+I_{2}{\sqrt {2}}\sin(2\omega t+\varphi _{22})+\dots$

där $\ U_{0}$ är likspänningskomponenten och $\ I_{0}$ är likströmskomponenten. Efter multiplikation och integrering kan medeleffekten skrivas som

$\ P=U_{0}I_{0}+U_{1}I_{1}\cos(\varphi _{1})+U_{2}I_{2}\cos(\varphi _{2})+U_{3}I_{3}\cos(\varphi _{3})+\dots$

där $\ \varphi _{1}=\varphi _{11}-\varphi _{21},\varphi _{2}=\varphi _{12}-\varphi _{22},\dots$.

Detta innebär att

Endast termer med samma frekvenskomponenter (samma multipler av $\ \omega t$) ger bidrag till medeleffekten.

Om exempelvis en sinusformad spänning påtrycks en icke-linjär tvåpol, med en icke sinusformad ström som följd, kommer vid beräkningen av tvåpolens medeleffekt endast strömmens grundton (som har samma frekvens som spänningen) att ha betydelse.

Skenbar effekt ges liksom vid sinusformad spänning och ström av strömmens och spänningens effektivvärden som

$\ S=UI$

Effektfaktorn ges som i det sinusformade fallet av

$\ PF={P \over S}$

men effektfaktorn är inte längre cosinus för en vinkel mellan spänning och ström.

Reaktiv effekt är odefinierad för icke sinusformad spänning och ström. I praktiken används ibland

$Q={\sqrt {S^{2}-P^{2}}}$

eller i analogi med det sinusformade fallet

$\ Q=U_{1}I_{1}\sin \varphi _{1}$

Om övertonshalten är låg blir resultaten i praktiken lika, men vid stora övertonshalter kan skillnaden bli betydande och med det förra värdet alltid större än det senare.

Analytisk behandling av stationära växelströmsförlopp

För analytisk behandling av stationära sinusformade växelströmsförlopp kan jω-metoden användas där varje impedans och växelstorhet representeras av ett komplext tal. Metoden ger vanligen betydande förenklingar då reglerna för likströmskretsar kan tillämpas på växelströmskretsar.

Enkla växelströmskretsar

Serieresonans

Serieresonanskrets Visardiagram för serieresonanskretsen För momentanvärdena i en serieresonanskrets gäller $u=Ri+L{\frac {di}{dt}}+{\frac {1}{C}}\int {i\,dt}$ Motsvarande ekvation i komplex form: ${\overline {U}}=\left(R+\mathrm {j} \omega L+{1 \over \mathrm {j} \omega C}\right){\overline {I}}$ Inför den komplexa spänningen och strömmen ${\overline {U}}=U\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\beta )}=U{\underline {/\beta }}\,$ ${\overline {I}}=I\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\alpha )}=I{\underline {/\alpha }}$ Härav $I={\frac {U}{\sqrt {R^{2}+\left(\omega L-{\cfrac {1}{\omega C}}\right)^{2}}}}$ $\alpha =\beta -\arctan {\frac {\omega L-{\cfrac {1}{\omega C}}}{R}}$ Impedansens absolutbelopp $|Z|={\sqrt {R^{2}+\left(\omega L-{\cfrac {1}{\omega C}}\right)^{2}}}$ och dess fasvinkel ${\underline {/Z}}=\arctan {\frac {\omega L-{\cfrac {1}{\omega C}}}{R}}$ Serieresonanser för olika Q-värden Om $\omega L>{\frac {1}{\omega C}}$ ligger spänningen före strömmen (induktiv fasförskjutning) och om $\omega L={\frac {1}{\omega C}}$ ligger spänningen i fas med strömmen och om $\omega L<{\frac {1}{\omega C}}$ ligger spänningen efter strömmen (kapacitiv fasförskjutning). Resonans inträffar för vinkelfrekvensen $\omega _{r}={\frac {1}{\sqrt {LC}}}$ Om kretsens godhetstal $Q_{r}={\frac {\omega _{r}L}{R}}$ är stort blir resonanskurvorna höga och spetsiga.

Parallellresonans

Parallellkrets Visardiagram för parallellkretsen. Spänningen är riktfas För momentanvärdena i en parallellresonanskrets gäller ekvationerna $i=i_{1}+i_{2}\,$ $u=Ri_{1}+L{\frac {di_{1}}{dt}}+{\frac {1}{C}}\int {i_{2}\,dt}$ Motsvarande ekvationer i komplex form: ${\overline {I}}={\overline {I}}_{1}+{\overline {I}}_{2}\,$ ${\overline {U}}=(R+\mathrm {j} \omega L){\overline {I}}_{1}={\frac {1}{\mathrm {j} \omega C}}{\overline {I}}_{2}$ Kretsens impedans $Z={\frac {\overline {U}}{\overline {I}}}={\cfrac {(R+\mathrm {j} \omega L){\cfrac {1}{\mathrm {j} \omega C}}}{R+\mathrm {j} (\omega L-{\cfrac {1}{\omega C}})}}={\cfrac {R+\mathrm {j} \omega L}{(1-\omega ^{2}LC)+\mathrm {j} \omega CR}}$ Resonanser när absolutbeloppet av Z är maximum I en parallellresonanskrets kan resonans definieras på olika sätt som leder till olika resonansfrekvenser. 1. Resonans inträffar vid den frekvens vid vilken serieresonans inträffar, $\omega _{1}=\omega _{r}={\frac {1}{\sqrt {LC}}}$ 2. Resonans inträffar vid den frekvens vid vilken ström och spänning ligger i fas, $\omega _{2}=\omega _{r}{\sqrt {1-{\frac {1}{Q_{r}^{2}}}}}$ 3. Resonans inträffar vid den frekvens vid vilken |Z| är maximal vid variation av frekvensen, $\omega _{3}=\omega _{r}{\sqrt {{\sqrt {1+{\frac {2}{Q_{r}^{2}}}}}-{\frac {1}{Q_{r}^{2}}}}}$ Qr är godhetstalet vid resonans eller $Q_{r}={\frac {\omega _{r}L}{R}}={\frac {1}{\omega _{r}CR}}$

Historik

Nikola Tesla var en av pionjärerna inom utvecklingen av växelströmssystem. Tesla gjorde växelströmmen mer allmänt användbar genom att konstruera den första växelströmsmotorn 1882 samt utvecklade transformatorn på ett sätt som möjliggjorde uppbyggnaden av dagens eldistributionsnät. Den första växelströmsgeneratorn var baserad på Michael Faradays principer och konstruerades av den franske instrumentmakaren Hippolyte Pixii 1832. Den första kommersiella tillämpningen av elektrisk energi - glödlampan - utnyttjade likström (likspänning). Likström som strömart kom därefter att utnyttjas under åtskilliga år. På grund av fördelar vid generering och distribution produceras elektrisk energi idag nästan enbart som växelströmsenergi. Efter konstruktionen av växelströmstransformatorn, en enkel och effektiv apparat utan rörliga delar, kunde det föregående likströmssystemet ej längre konkurrera. Dessutom konstruerades den robustaste och tillförlitligaste elmotorn av alla – den kortslutna asynkronmotorn – för växelströmsdrift.

Att växelströmmen kommit att bli den dominerande strömarten innebär inte att likströmmen är betydelselös. Exempelvis sker ofta överföringen av mycket stora effekter över långa avstånd med högspänd likström (HVDC = high voltage direct current). I generatorstationerna omvandlas växeleffekten till likströmseffekt. Likströmsegenskaperna (låga förluster) utnyttjas sedan under själva överföringen och energin omvandlas på mottagarsidan tillbaka till växelströmsenergi. Ytterligare exempel där likström är en attraktiv strömart är vid motordrift med högt ställda krav på möjligheterna att exempelvis styra och kontrollera startförlopp och varvtal. I vissa fall är likström den enda möjliga strömarten, till exempel för elektrokemiska processer.

Se även

• Trefassystem
• Tvåfassystem
• Enfassystem
• jω-metoden
• Faskompensering
• Likström
• Växelspänning
• Nätverksanalysator
• Hällsjön, Smedjebackens kommun, världens första kommersiella kraftöverföring för växelström, invigd 1893.

Referenser

• Klaus Lunze: Theorie der Wechselstromschaltungen, Verlag Technik, Berlin 1991, ISBN 3-341-00984-1

Externa länkar

• Wikimedia Commons har media som rör Växelström.
  Bilder & media