Millerindex

Exempel på riktningar angivna med Millerindices.

Plan med olika Millerindices i kubiska kristaller.

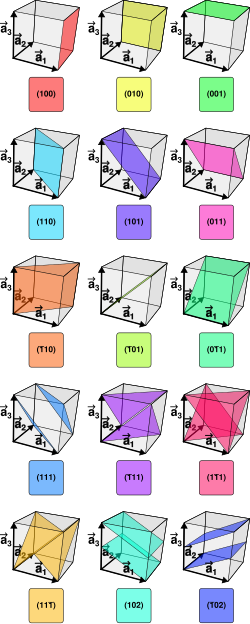
Millerindex används inom fasta tillståndets fysik för att beteckna olika riktningar och plan i kristallstrukturer. Systemet publicerades 1839 av den brittiska mineralogen William Hallowes Miller. Hans index består av tre heltal hkl (eller lmn, om man så vill). Negativa heltal anges med ett streck över talet, se figur. Systemet bygger på kristallaxlar. I icke-kubiska kristaller skiljer det sig starkt från det kartesiska koordinatsystemet.

Riktning [hkl ] och ekvivalenta riktningar <hkl >

Om man vill ange en riktning, utgår man från kristallstrukturens basvektorer, se figur. Riktningen [100] (uttal: "ett noll noll") är parallell med kristallens x-riktning. På samma sätt är [010] parallell med kristallens y-riktning, som inte behöver vara vinkelrät mot [100]. Negativa riktningar anges med ett streck över talet. Observera att $[1{\bar {1}}0]$ inte är ekvivalent med $[{\bar {1}}10]$, till exempel är i det allmänna fallet avstånden mellan gitterpunkter olika i dessa två riktningar.

I ett kubiskt gitter är riktningen [100] fysikaliskt likvärdigt med [010], [001], [100], osv. De går alla utmed en av kubens kanter. Skillnaden beror bara på valet av koordinatsystem. Samlingen av alla dessa riktningar är <100>. På samma sätt representerar <110> kubens ytdiagonaler och <111> kroppsdiagonalerna.

Kristallplan (hkl ) och ekvivalenta plan {hkl }

För att tala om kristallytor och särskilt för att tala om röntgendiffraktion behöver man ett sätt att beskriva dem. Särskilt enkla är kubiska gitter, eftersom Millerindex då är lika med riktningen på planets normal. Ett exempel är de tätpackade ytor i fcc-kristaller, som är vinkelräta mot kubens kroppsdiagonal med riktning [111]. Planet har då Millerindex (111). På grund av fcc-kristallens symmetri är alla tätpackade plan ekvivalenta. Mängden av alla plan ekvivalenta med denna anges {111}.

Två exempel på bestämning av Millerindex för kristallplan: (111) och (221)

I det allmänna fallet är Millerindex för kristallplan definierade genom en procedur där man först bestämmer planets skärningspunkter med kristallaxlarna. Man tar de reciproka värdena av dessa och multiplicerar med en gemensam faktor för att få tre heltal. I det första exemplet till vänster skär planet axlarna i de tre gitterpunkterna närmast origo. De reciproka värdena är då också heltalen 1,1,1, så att planets beteckning är (111). I det andra exemplet i figuren till vänster skär planet axlarna vid x=½, y=½, z=1. De reciproka värdena är heltalen 2,2,1, så att det är ett (221)-plan. Valet av origo spelar ingen roll: vid ett annat val ligger skärningspunkterna vid x=1, y=1, z=2. De reciproka värdena blir nu 1,1,½. Multiplikation med en gemensam faktor ger samma index (221).

Plan som ligger parallella med en eller två axlar, har skärningspunkter i oändligheten, med det reciproka värdet noll.

Röntgendiffraktion

Röntgendiffraktion kan beskrivas som interferens av reflektioner från kristallplan med inbördes avstånd d. I en kubisk struktur gäller att d = a/√(h ² + k ² + l ²). Det betyder att Millerindex (002) inte motsvarar samma diffraktion som (001), även om de är ekvivalenta när vi talar om kristallytor (detta står klart ty avståndet d uträknat ur formeln kan bli godtyckligt litet genom att välja h tillräckligt stort i beteckningen (hkl) och kan alltså inte svara mot ett fysikaliskt avstånd). Tolkat i fysikaliska plan (plan som innehåller atomer) är i själva verket beteckningen (002) att utläsas som andra ordningens diffraktion mellan atomerna i parallella (001)-plan. Braggs lag innehåller nämligen en heltalsmultipel n (diffraktionsordning) som härmed har införlivats i det inbördes avståndet d som därmed omtolkas. På detta vis erhålles endast en obekant i Braggs lag. Det framgår oftast av sammanhanget huruvida man avser Millerindex för refraktioner eller för ytor.

Referenser

• Kittel, Charles. Introduction to Solid State Physics. John Wiley & Sons, Inc., eighth edition, 2005.