Enkel funktion
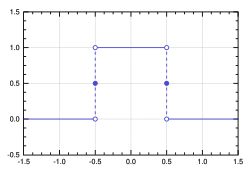
En enkel funktion är inom matematisk analys en funktion som endast antar ett ändligt antal värden. Ett enkelt exempel är takfunktionen på intervallet som endast antar värden . Ett annat exempel är Dirichlets funktion som endast antar värden 0 (för irrationella tal) och 1 (för rationella tal). Enkla funktioner används i första stadiet av konstruktionen av exempelvis Lebesgueintegralen, då det är väldigt lätt att integrera över en enkel funktion.
Definition
[redigera | redigera wikitext]En enkel funktion kan uttryckas som en linjärkombination av indikatorfunktioner, , av mätbara mängder. Om är ett mätbart rum, är en följd av mätbara mängder och en följd av tal, är
en enkel funktion.
Egenskaper
[redigera | redigera wikitext]Summor, skillnader och produkter av enkla funktioner är återigen enkla funktioner, så att mängden av alla enkla funktioner bildar en kommutativ algebra över en kropp.
För varje icke-negativ mätbar funktion f från ett måttrum X till de reella talen existerar det en följd av enkla funktioner så att
likformigt när .
Integration
[redigera | redigera wikitext]Om är ett måttrum, så är integralen av en enkel funktion med avseende på :
om alla summander är ändliga.
Referenser
[redigera | redigera wikitext]- Walter, Rudin (1987). Real and Complex Analysis. McGraw-Hill. ISBN 0-07-100276-6

![{\displaystyle [0,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363608267ac9a1e7499c838386bbc69779637cd8)












