Caesarchiffer

Inom kryptologi är Caesarchiffer, Caesarkryptot eller Caesarrullning en form av chiffer, närmare bestämt en av den första kända formen av substitutionschiffer. Idag låter många begreppet Caesarchiffer stå för en rad olika alfabetiska substitutioner. Den är ett av de enklaste chiffren men principen kan ge mer komplexa kodningar som Vigenère-chiffret och det fortfarande moderna triviala ROT13 systemet. Det är en av de mest kända krypteringarna men erbjuder föga kommunikationssäkerhet i modern tid.
Historia
[redigera | redigera wikitext]
Caesarchiffret har fått sitt namn för att hedra Julius Caesar som var en flitig användare av krypterade meddelanden. Han använde chiffret för att kommunicera med Cicero och andra vänner i Rom samt för militära ändamål. Det första exemplet på substitutionschiffer i krigföring finns i Julius Caesars skildring av fälttågen i Gallien. Där beskrivs hur Cicero, omringad och nära att ge upp, mottar ett krypterat meddelande från Caesar efter ett dramatiskt överlämnande.
| ” | Budbäraren instruerades att, om han inte kunde nå ända fram, slunga sitt spjut med brevet fastsatt vid läderremmen, in över befästningen i lägret... Då gallern vädrade fara, avlossade han spjutet, som han blivit tillsagd. Det råkade fastna i tornet, och förblev i två dagar utom synhåll för de våra i hären; På tredje dagen siktades det av en soldat, hämtades ner och avlämnades till Cicero. Han läste igenom det och föredrog det sedan vid en truppmönstring, varvid alla storligen fröjdade sig. | „ |
| – [1] | ||
Caesar var beroende av att kunna kommunicera effektivt för att styra länder han erövrade och kommendera sina arméer, samtidigt var han väl medveten om vad som kunde hända om viktig information hamnade i fel händer. Han använde chiffer flitigt och växlade mellan flera olika. Systemet var så omfattande att Probus skrev en hel avhandling om de olika chiffren som tyvärr gått förlorad. Tack vare Suetonius arbete "åtta böcker om tolv kejsares liv" finns dock en utförlig beskrivning av chiffren kvar. Han nämner dock bara fallet i exemplet ovan då bokstaven förskjuts tre steg framåt men det är självklart att vilka steg som helst kan användas. Om man inte begränsar sig till förskjutning utan tillåter vilka som helst motsvarigheter mellan bokstäverna (substitutionschiffer), så får vi (med ett alfabet på 26 bokstäver) ungefär 4·1026 möjliga arrangemang.[2]
Avkodning
[redigera | redigera wikitext]Att avkoda eller forcera Caesarchiffer är idag en lätt uppgift. Det är en kraftlös kryptering eftersom det bara finns ett litet antal möjliga nycklar. I fallet där varje bokstav ersätts med en ett visst antal steg framåt i alfabetet, finns (om man använder det svenska alfabetet) bara 28 möjliga nycklar (utöver den triviala 0 eller 29, som inte förändrar texten). Avkodningen kan utföras enkelt med totalsökning eller statistisk analys – eller helt enkelt genom att gissa vad de kortaste orden står för. Eftersom ordningen av bokstäverna i klartexten behålls och endast byter namn så finns strukturen kvar i kryptotexten. Detta gör det särskilt lätt att avkoda en längre text.
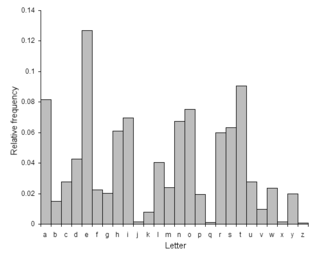
För att forcera ett Ceasarchiffer står fienden inför ett antal utmaningar. Han kan till exempel veta eller gissa att det handlar om ett substitutionschiffer men inte att det är just av denna substitutionstyp. Eller så vet han att det är ett Ceasarchiffer men inte vad stegvärdet är. I det första fallet kan metoden Frekvensanalys användas för att fienden snabbt ska se ett mönster. I det andra fallet finns det bara ett begränsat antal steg och de kan testas i en så kallas Brute forceattack.
Chiffret kan ses som en kombination av en allmän krypteringsmetod, en algoritm, och en del som bestämmer detaljerna i varje enskilt fall, en nyckel. I ovan nämnda fall är algoritmenattr man ersätter bokstaven i klartextalfabetet med bokstaven i kryptoalfabetet, som kan innehålla vilken stegändring som helst. Nyckelns roll är då att bestämma exakt vilket kryptoalfabet som används för krypteringen.
- Förhållandet mellan nyckel och algoritm.
Nyckel + klartext → Algoritm → KRYPTOTEXT Nyckel + KRYPTOTEXT → Algoritm → klartext
Fienden kan ofta ha en misstanke om vilken algoritm det handlar om och misstänka att bokstäverna i klartexten blivit ersatt med bokstäver ur kryptotexten. Dock är det föga troligt att han vet vilken nyckel som har använts för att kryptera meddelandet och detta kräver då vidare undersökning.
Modern användning
[redigera | redigera wikitext]Caesarchiffret används fortfarande i ROT13-chiffret, där nyckeln är 13 och alfabetet det engelska. Detta finns som funktion i många e-post-klienter och motsvarande program. Idén är då inte att använda chiffret för kryptering, utan för att dölja klartexten, antingen för att den kan vara stötande (lättstötta kan då låta bli att läsa den), eller för att den innehåller något som inte genast skall avslöjas, t.ex. lösningen på en gåta ("Usenets motsvarighet till att skriva klurighetslösningar uppochner i en tidning"[3]).
Se även
[redigera | redigera wikitext]Referenser
[redigera | redigera wikitext]- ^ Singh 1999, s. 24.
- ^ Singh 1999, s. 26.
- ^ Usenet-post av Bruce Horrocks "It's the Usenet equivalent of a magazine printing the answer to a quiz upside down."
Källor
[redigera | redigera wikitext]- Newton, David E. (1997) (på engelska). Encyclopedia of cryptology. Santa Barbara: ABC-Clio. Libris 6205528. ISBN 0-87436-772-7
- Singh, Simon (1999). Kodboken. Stockholm: Norstedt. Libris 8345451. ISBN 91-1-300708-4
- Wobst, Reinhard (2001) (på engelska). Cryptology Unlocked. Chichester: John Wiley & Sons. Libris 10596661. ISBN 978-0-470-06064-3
- Kryptologi i Nationalencyklopedins nätupplaga.
