Nod (fysik)
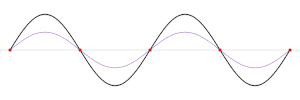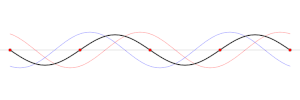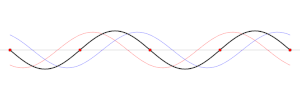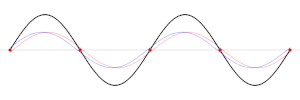
En nod är i fysiken en punkt i en stående våg med minst amplitud, och som i teorin står stilla. Exempelvis på en vibrerande gitarrsträng är ändarna av strängen noder. Genom att ändra positionen för slutnoden genom band, ändrar gitarristen den effektiva längden på den vibrerande strängen och därmed den spelade tonen. Motsatsen till en nod är en anti-nod, en punkt där amplituden för den stående vågen är maximal. Dessa inträffar mitt emellan noderna.[1]
Förklaring
[redigera | redigera wikitext]
Stående vågor uppstår när två sinusformade vågtåg med samma frekvens rör sig i motsatta riktningar i samma utrymme och interfererar med varandra.[2] De uppstår när vågor reflekteras vid en gräns, såsom ljudvågor som reflekteras från en vägg eller elektromagnetiska vågor som reflekteras från slutet av en transmissionsledning, och särskilt när vågor är instängda i en resonator vid resonans och studsar fram och tillbaka mellan två gränser, till exempel i en orgelpipa eller gitarrsträng.
I en stående våg är noderna en serie platser med jämnt fördelade intervall där vågamplituden (rörelsen) är noll (se animationen ovan). Vid dessa punkter adderas de två vågorna med motsatt fas och tar ut varandra. De förekommer med intervaller på en halv våglängd (λ/2). Mitt emellan varje par av noder finns platser där amplituden är maximal. Dessa kallas antinoder. Vid dessa punkter adderas de två vågorna med samma fas och förstärker varandra.
I de fall där de två motsatta vågtågen inte har samma amplitud, avbryter de inte perfekt, så amplituden för den stående vågen vid noderna är inte noll utan bara ett minimum. Detta inträffar när reflektionen vid gränsen är ofullkomlig. Detta visas av ett ändligt stående vågförhållande (SWR), förhållandet mellan amplituden för vågen vid antinoden och amplituden vid noden.
I resonans av en tvådimensionell yta eller membran, såsom ett trumskinn eller en vibrerande metallplatta, blir noderna nodlinjer, linjer på ytan där ytan är orörlig, som delar ytan i separata områden som vibrerar med motsatt fas. Dessa kan göras synliga genom att strö sand på ytan, och de invecklade mönstren av linjer som blir resultatet kallas Chladni-figurer.
I transmissionsledningar är en spänningsnod en strömantinod och en spänningsantinod är en strömnod.
Noder är punkterna med nollförskjutning, inte punkterna där två ingående vågor skär varandra.
Gränsförhållanden
[redigera | redigera wikitext]Var noderna uppstår i förhållande till gränsen som reflekterar vågorna beror på slutförhållandena eller gränsvillkoren. Även om det finns många typer av slutförhållanden är ändarna på resonatorer vanligtvis en av två typer som orsakar total reflektion:
- Fast gräns: Exempel på denna typ av gräns är fästpunkten för en gitarrsträng, den slutna änden av ett öppet rör som en orgelpipa, eller en träblåspipa, periferin av ett trumskinn, en transmissionsledning med kortsluten ände, eller speglarna i ändarna av en laserkavitet. I denna typ tvingas vågens amplitud till noll vid gränsen, så det finns en nod vid gränsen, och de andra noderna förekommer vid multiplar av en halv våglängd från den:
- 0, λ/2, λ, 3λ/2, 2λ, ..., nλ/2
- Fri gräns: Exempel på denna typ är en orgel med öppen ände eller träblåspipa, ändarna på de vibrerande resonatorstängerna i en xylofon, klockspel eller stämgaffel, ändarna på en antenn eller en transmissionsledning med en öppen ände. I denna typ tvingas derivatan (lutningen) av vågens amplitud (i ljudvågor trycket, i elektromagnetiska vågor, strömmen) till noll vid gränsen. Så det finns ett amplitudmaximum (antinod) vid gränsen, den första noden inträffar en kvarts våglängd från slutet, och de andra noderna är med halva våglängdsintervall därifrån:
- λ/4, 3λ/4, 5λ/4, 7λ/4, ..., (2n+1)λ/4
Exempel
[redigera | redigera wikitext]Ljud
[redigera | redigera wikitext]En ljudvåg består av alternerande cykler av kompression och expansion av vågmediet. Under kompressionen tvingas mediets molekyler samman, vilket resulterar i det ökade trycket och densiteten. Under expansionen tvingas molekylerna isär, vilket resulterar i minskat tryck och densitet.
Antalet noder i en specificerad längd är direkt proportionell mot vågens frekvens.
Ibland på en gitarr, fiol eller annat stränginstrument används noder för att skapa övertoner. När fingret placeras ovanpå strängen vid en viss punkt, men inte trycker strängen hela vägen ner till greppbrädan, skapas en tredje nod (utöver bryggan och skruven) och en harmonisk ton ljuder. Under normalt spel när banden används är övertonerna alltid närvarande, även om de är tystare. Med den artificiella nodmetoden är övertonen högre och den grundläggande tonen är tystare. Om fingret placeras i mitten av strängen hörs den första övertonen, som är en oktav över grundtonen som skulle spelas om övertonen inte hade ljudit. När ytterligare två noder delar upp strängen i tredjedelar, skapar detta en oktav och en perfekt kvint (tolfte). När ytterligare tre noder delar upp strängen i fjärdedelar, skapar detta en dubbel oktav. När ytterligare fyra noder delar upp strängen i femtedelar, skapar detta en dubbeloktav och en stor ters (17:e). Oktaven, durters och perfekt kvint är de tre tonerna som ingår i ett durakord.
Det karakteristiska ljudet som gör att lyssnaren kan identifiera ett visst instrument beror till stor del på den relativa storleken på de övertoner som skapas av instrumentet.

Vågor i två eller tre dimensioner
[redigera | redigera wikitext]
I tvådimensionella stående vågor är noder kurvor (ofta raka linjer eller cirklar när de visas på enkla geometrier.) Till exempel samlas sand längs noderna på en vibrerande Chladni-platta för att indikera områden där plattan inte rör sig.[3]
Inom kemi används kvantmekaniska vågor, eller "orbitaler", för att beskriva vågliknande egenskaper hos elektroner. Många av dessa kvantvågor har också noder och antinoder. Antalet och placeringen av dessa noder och antinoder ger upphov till många av egenskaperna hos en atom eller kovalent bindning. Atomorbitaler klassificeras enligt antalet radiella och vinkelnoder. En radiell nod för väteatomen är en sfär som uppstår där vågfunktionen för en atomomloppsbana är lika med noll, medan vinkelnoden är ett platt plan.[4]
Molekylära orbitaler klassificeras efter bindningskaraktär. Molekylära orbitaler med en antinod mellan kärnor är mycket stabila, och är kända som "bindande orbitaler" som stärker bindningen. Däremot kommer molekylära orbitaler med en nod mellan kärnor inte att vara stabila på grund av elektrostatisk repulsion och är kända som "antibindande orbitaler" som försvagar bindningen. Ett annat sådant kvantmekaniskt koncept är partikeln i en låda där antalet noder för vågfunktionen kan hjälpa till att bestämma kvantenergitillståndet – noll noder motsvarar grundtillståndet, en nod motsvarar det 1:a exciterade tillståndet, etc. I allmänhet,[5] Om man ordnar egentillstånden i ordningen med ökande energier, , sjunker egenfunktionerna likaledes i ordningen med ökande antal noder. Den n:te egenfunktionen har n−1 noder, mellan var och en av dessa har följande egenfunktioner minst en nod.
Se även
[redigera | redigera wikitext]Referenser
[redigera | redigera wikitext]- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Node (physics), 12 mars 2023.
Noter
[redigera | redigera wikitext]- ^ Stanford, A. L.; Tanner, J. M. (2014). Physics for Students of Science and Engineering. Academic Press. sid. 561. ISBN 978-1483220291. https://books.google.com/books?id=XONbAwAAQBAJ&dq=antinode+%22midway+between+nodes%22&pg=PA561
- ^ Feynman, Richard P.; Robert Leighton; Matthew Sands (1963). ”Modes”. The Feynman Lectures on Physics, Vol.1. USA: Addison-Wesley. ISBN 0-201-02011-4
- ^ Comer, J. R., et al. "Chladni plates revisited." American journal of physics 72.10 (2004): 1345-1346.
- ^ Supplemental modules (physical and Theoretical Chemistry). Chemistry LibreTexts. (2020, December 13). Retrieved September 13, 2022, from https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)
- ^ Albert Messiah, 1966. Quantum Mechanics (Vol. I), English translation from French by G. M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III. online Ch 3 §12
Externa länkar
[redigera | redigera wikitext]

